[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
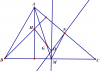
1.Cho tam giác ABC. Gọi M là trung điểm của cạnh BC. N là trung điểm của cạnh AC. Các đường trung trực của cạnh AC và BC cắt nhau tại O; H là trực tâm và G là trong tâm của tam giác. CMR:
a) tam giác ABH đồng dạng tam giác MNO
b) tam giác AHG đồng dạng tam giác MOG
c) Ba điểm H, G, O thẳng hàng và OH=3OG
2. Cho [tex]\Delta ABC [/tex] đồng dạng [TEX]\Delta A'B'C' [/TEX]biết [TEX]\frac{A'B'}{AB}=\frac{4}{7}.[/TEX] Chu vi của tam giác A'B'C' là 48m. Các cạnh của tam giác ABC tỉ lệ với 2:3:5
a) Tính chu vi của tam giác ABC
b) Tính các cạnh của tam giác ABC
Giúp với , cần gấp lắm ạ!!
a) tam giác ABH đồng dạng tam giác MNO
b) tam giác AHG đồng dạng tam giác MOG
c) Ba điểm H, G, O thẳng hàng và OH=3OG
2. Cho [tex]\Delta ABC [/tex] đồng dạng [TEX]\Delta A'B'C' [/TEX]biết [TEX]\frac{A'B'}{AB}=\frac{4}{7}.[/TEX] Chu vi của tam giác A'B'C' là 48m. Các cạnh của tam giác ABC tỉ lệ với 2:3:5
a) Tính chu vi của tam giác ABC
b) Tính các cạnh của tam giác ABC
Giúp với , cần gấp lắm ạ!!
Last edited by a moderator: