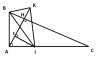
* Để tìm số đo của 1 góc, ta nghĩ đến cách cộng tất cả các góc nhỏ hơn tại thành góc đó nhưng đề bài lại không cho các góc cụ thể. Cảm quan ta thấy, góc BKI vuông tại K. [tex]\Leftrightarrow[/tex] Chứng minh theo định lý Pytago cho tam giác BKI dựa vào số đo các cạnh đề bài cho
Kẻ IE vuông góc với AH tại I
IE vuông góc với AH
BC vuông góc AH
[tex]\Leftrightarrow[/tex] IE song song BC
[tex]\Leftrightarrow \frac{AE}{AH}=\frac{AI}{AC}=\frac{1}{3}[/tex]
[tex]\Rightarrow AE = \frac{1}{3}AH = HK[/tex]
[tex]\Rightarrow AH=EK[/tex]
Chứng minh tam giác BKI thỏa mãn Pytago
[tex]BI^2 = BA^2 + AI^2 =(AH^2+BH^2)+(AE^2+EI^2)[/tex]
[tex]=(AH^2+EI^2)+(BH^2+AE^2) = (EK^2+EI^2)+(BH^2+HK^2)[/tex]
[tex]= IK^2+BK^2 (T/m)[/tex]
Suy ra [tex]\widehat{BKI} = 90[/tex] độ
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
