Cho tam giác ABC có [tex]\widehat{B}=70^{\circ},\widehat{C}=60^{\circ}[/tex] và tâm đường tròn ngoại tiếp là O. Đường thẳng BO cắt AC tại D và đường thẳng CO cắt AB tại E. Tính [TEX]\widehat{OED}[/TEX].
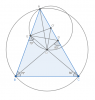
Gọi $O'$ là tâm đường tròn ngoại tiếp $\triangle{AEO}$
Tính $\widehat{AEO} = 140^\circ$
$\widehat{AO'O} = 2(180 - \widehat{AEO}) = 140^\circ$ (góc ở tâm - góc nội tiếp)
$\widehat{O'AO} = 90^\circ - \dfrac12 \widehat{AO'O} = 20^\circ$ (tam giác cân)
Tính $\widehat{AOC} = 2 \widehat{ABC} = 140^\circ$ (góc ở tâm - góc nội tiếp)
$\widehat{OAC} = 90^\circ - \dfrac12 \widehat{AOC} = 20^\circ$
Suy ra $O', A, C$ thẳng hàng (do $\widehat{O'AO} = \widehat{CAO}$)
Tính $\widehat{O'EA} = \widehat{O'AE} = 50^\circ$
$\widehat{O'EO} = 180^\circ - \widehat{AEO'} - \widehat{BEC} = 60^\circ$
Suy ra $\triangle{O'EO}$ là tam giác đều (tam giác cân có 1 góc $60^\circ$)
Tính $\widehat{DO'O} = 2\widehat{OAC} = 40^\circ$
$\widehat{DOO'} = \widehat{CDO} - \widehat{DO'O} = 40^\circ$
Suy ra $\triangle{DOO'}$ cân tại $D$
Từ đó $\triangle{O'DE} = \triangle{ODE}$, suy ra $\widehat{OED} = \dfrac12 \widehat{OEO'} = 30^\circ$
Đôi lời: Các bài toán tính góc này
không phải là chuyện đùa và đối với mình, tìm lời giải THCS cho nó rất là mệt -_- (nếu giải bằng lượng giác thì vài dòng).
Mình vừa giải bằng cách lớp 9, không rõ là kiến thức HKI hay HKII nhưng mình hy vọng là bạn hiểu được và đừng bảo "chưa học". Mình sẽ không giải lại đâu, tốn quá nhiều thời gian và mình không có nhiều thời gian.
Bài này có thể giải bằng cách lớp 7 không?
Chắc chắn là có. Nhưng mình nói ở trên rồi, mình không có thời gian để tìm thêm những cách đẹp hơn.
Chuyện nghiên cứu cách khác mình sẽ để lại cho bạn nhé. Có 1 lớp bài toán bạn có thể tham khảo:
Bài toán về tam giác 80-80-20.
Cảm ơn bạn!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
