Dạ em cảm ơn chị ạ, dạ cho em hỏi là làm sao từ hệ thức tỉ lệ giữa R1, R2, R3 và R4 ta có thể suy ra được mạch cầu câng bằng (ý em là chứng minh phần đảo ạ, phần thuận thì em hiểu rồi ạ).
II, Chứng minh theo chiều nghịch
Ta có: [tex]\frac{R_1}{R_2}=\frac{R_3}{R_4}=n[/tex][tex]\Rightarrow \left\{\begin{matrix} R_1=nR_2\\ R_3=nR_4 \end{matrix}\right.[/tex]
Chúng ta sẽ biến đổi mạch tam giác thành mạch sao, cụ thể như hình:
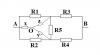
Khi đó:
[tex]\left\{\begin{matrix} z=\frac{R_1R_5}{R_1+R_2+R_5}\\ y=\frac{R_2R_5}{R_1+R_2+R_5} \end{matrix}\right.[/tex]
(Tại sao có điều này thì xem ở topic hướng dẫn dò mạch chị có hướng dẫn rồi nhé)
Mạch lúc này trở thành: [tex]xnt[(zntR_3)//(yntR_4)][/tex]
Ta có hệ thức:
[tex]U_3=\frac{U_{OB}R_3}{z+R_3}=\frac{U_{OB}.R_3(R_1+R_2+R_5)}{R_1R_5+R_3(R_1+R_2+R_5)}=\frac{U_{OB}.n.R_4(R_1+R_2+R_5)}{nR_2R_5+n.R_4(R_1+R_2+R_5)}=\frac{U_{OB}.R_4(R_1+R_2+R_5)}{R_2R_5+R_4(R_1+R_2+R_5)}[/tex]
Mà : [tex]U_4=\frac{U_{OB}R_4}{y+R_4}=\frac{U_{OB}.R_4(R_1+R_2+R_5)}{R_2R_5+R_4(R_1+R_2+R_5)}[/tex]
[tex]\Rightarrow U_3=U_4\Rightarrow I_5=0(dpcm)[/tex]
Xem chi tiết tại :
[Vật lí] Chuyên đề mạch cầu
Chúc em học tốt, có gì thắc mắc em có thể hỏi lại.
Xem thêm:
Thiên đường vật lý
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
