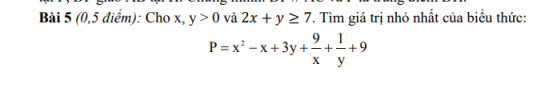Bài này phải dùng giả điểm rơi nhé, giả sử khi dấu = xảy ra thì [imath]x= a \Rightarrow y = 7 - 2a[/imath]
Khi đó , ta cần dự đoán chỗ sử dụng cosi, có 3 chỗ:
B1: Hạ từ [imath]x^2 \rightarrow x[/imath], ta dùng : [imath]x^2 + a^2 \geq 2ax[/imath]
Lúc này đang có [imath](2a-1)x[/imath]
B2: Ghép [imath]\dfrac{9}{x}[/imath] với 1 lượng x là [imath]mx[/imath] bằng cosi.
Khi đó dấu = xảy ra khi [imath]\dfrac{9}{x} =mx \Rightarrow m = \dfrac{9}{x^2} = \dfrac{9}{a^2}[/imath]
Vậy sau B2 còn dư [imath](2a-1 - \dfrac{9}{a^2}) x[/imath]
B3: Ghép [imath]\dfrac{1}{y}[/imath] với 1 lượng y là [imath]ny[/imath] bằng cosi.
Khi đó dấu = xảy ra khi [imath]\dfrac{1}{y} =ny\Rightarrow n = \dfrac{1}{y^2} = \dfrac{1}{(7-2a)^2}[/imath]
Vậy sau B3 còn dư [imath](3 - \dfrac{1}{(7-2a)^2}) y[/imath]
B4: sử dụng giả thiết [imath]2x+y \geq 7[/imath]
Lúc này để sử dụng được thì : [imath]\dfrac{2a-1 - \dfrac{9}{a^2} }{2} = 3 - \dfrac{1}{(7-2a)^2}[/imath]
Chỗ này thì mk ấn máy tính ra [imath]a=3[/imath], bạn thử = thay số vào cũng được.
Vậy giống bài của bạn
@Beo'S cùng kết điểm rơi [imath]x=a=3[/imath]nhỉ ^^
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
