Toán 9 SPHN 2019-2020

[Duy Quang Vũ 2007]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Mình xin gửi đến các bạn một bài hình học "nhẹ nhàng" chào đón năm mơi nhé!

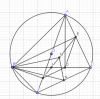
Cho tam giác ABC nhọn nội tiếp (O) và AB>AC.
D,E lần lượt là chân đường cao tam giác ABC hạ từ A và B
F là chân đường vuông góc hạ từ B lên AO
a. Chứng minh B,D,E,F là bốn đỉnh của một hình thang cân
b. EF đi qua trung điểm BC
c. Gọi P là giao điểm thứ hai của AO và (O); M và N lần lượt là trung điểm EF và CP
Tính [tex]\widehat{BMN}[/tex]

 

[Alice_www]

a) Ta có $\widehat{AFB}=\widehat{ADB}=\widehat{AEB}=90^\circ$
$\Rightarrow A,E,D,F,B$ cùng thuộc một đường tròn
$\Rightarrow \widehat{BAF}=\widehat{BEF};\: \widehat{EBD}=\widehat{DAE}$ (cùng chắn 1 cung)
Ta có: $\widehat{EBD}=\widehat{DAE}=90^\circ-\widehat{ADC}$
$=90^\circ-\widehat{ACD}=90^\circ-\widehat{APB}=\widehat{BAP}=\widehat{BDF}$
$\Rightarrow BE//FD$ và $ED=BF$
$\Rightarrow BEDF$ là hình thang cân
b) Gọi I là giao điểm của BC và EF
Suy ra$IB=IE\Rightarrow \Delta IBE$ cân tại $I\Rightarrow \widehat{IBE}=\widehat{IEB}$
Mà $\widehat{IEB}+\widehat{IEC}=90^\circ;\: \widehat{EBI}+\widehat{ECB}=90^\circ$
Suy ra $\widehat{IEC}=\widehat{ECB}\Rightarrow \Delta IEC$ cân tại $I$
Vậy $I$ là trung điểm của $BC$ ($IE=IC=IB$)
Hay $EF$ đi qua trung điểm của $BC$
c) $\widehat{BEF}=\widehat{BAF}=\widehat{BCP}$
$\widehat{EBC}=\widehat{BAF}=\widehat{BPF}$
Mà $\widehat{EBF}=\widehat{EBC}+\widehat{CBF}$
$\widehat{CBP}=\widehat{BPF}+\widehat{CBF}$
Suy ra $\widehat{EBF}=\widehat{CBP}$
Xét $\Delta BFE$ và $\Delta BPC$
có $\widehat{BEF}=\widehat{BCP};\: \widehat{EBF}=\widehat{CBP}$
$\Rightarrow \Delta BFE\sim \Delta BPC$
$\Rightarrow \dfrac{BF}{BP}=\dfrac{EF}{PC}=\dfrac{EM}{PN}$ và $\widehat{EFB}=\widehat{BPC}$
Suy ra $ \Delta BFM\sim \Delta BPN$
$\Rightarrow \widehat{MBF}=\widehat{NBP}\Rightarrow \widehat{MBN}=\widehat{PBF}$
Suy ra $ \Delta MBN\sim \Delta FBP\Rightarrow \widehat{BMN}=\widehat{BFP}=90^\circ$

Có gì khúc mắc em hỏi lại nhé
Ngoài ra em có thể tham khảo thêm ở topic này để ôn thi học kì nhé <3
https://diendan.hocmai.vn/threads/tong-hop-topic-on-thi-hoc-ki.841342/