 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1
Tìm số nguyên tố p sao cho p vừa là tổng của hai số nguyên tố vừa là hiệu của 2 số nguyên tố.
Bài 2 (Trung tâm là bài này)
Tìm tất cả các cặp số (p,q) thỏa mãn: p3-q5=(p+q)2
(Bài này mình đã tra trên mạng rồi nhưng họ làm tắt quá,mình không hiểu.Mong các bạn mà làm bài này hãy trình bày đầy đủ cho mình hiểu nhé!Cảm ơn)
Bài 3
Tìm x,y là các số dương để
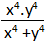 là số nguyên tố nhỏ nhất có thể
là số nguyên tố nhỏ nhất có thể
Tìm số nguyên tố p sao cho p vừa là tổng của hai số nguyên tố vừa là hiệu của 2 số nguyên tố.
Bài 2 (Trung tâm là bài này)
Tìm tất cả các cặp số (p,q) thỏa mãn: p3-q5=(p+q)2
(Bài này mình đã tra trên mạng rồi nhưng họ làm tắt quá,mình không hiểu.Mong các bạn mà làm bài này hãy trình bày đầy đủ cho mình hiểu nhé!Cảm ơn)
Bài 3
Tìm x,y là các số dương để

