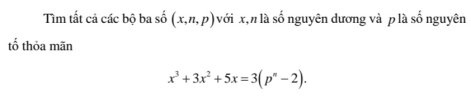Nếu a, b, m là các số nguyên dương (m ≤ n) thì [imath]ab = p^n \leftrightarrow \begin{cases} a = p^m \\ b = p^{n-m} \end{cases}[/imath] (C)
[imath]x^3 + 3x^2 + 5x = 3(p^n - 2) \newline \leftrightarrow \cfrac{1}{3} (x^3 + 3x^2 + 5x + 6) = p^n \newline \leftrightarrow \cfrac{1}{3} (x + 2)(x^2 + x + 3) = p^n[/imath]
Với k là số tự nhiên, để vế trái là số nguyên dương, ta có 2 TH:
(Ký hiệu a | b nghĩa là b chia hết cho a.)
[imath]\begin{array}{ll} 3 \mid x + 2 & \leftrightarrow x = 3k + 1 (k \ge 0) \leftrightarrow (k+1)(9k^2 + 9k + 5) = p^n (1) \\ 3 \mid x^2 + x + 3 & \leftrightarrow \begin{array}{ll} x = 3k + 2 & (k \ge 0) \leftrightarrow (3k+4)(3k^2 + 5k + 3) = p^n (2) \\ x = 3k & (k > 0) \leftrightarrow (3k+2)(3k^2 + k + 1) = p^n (3) \end{array} \end{array}[/imath]
(1): [imath]\cfrac{9k^2+9k+5}{k+1} = 9 + \cfrac{5}{k+1}[/imath] nguyên khi k = 0 (thỏa (C)) ∨ k = 4 (không thỏa (C)) → k = 0 → (x, n, p) = (1, 1, 5)
(2): [imath]\cfrac{3k^2+5k+3}{3k+4} = \cfrac{(3k+4) \left ( k+\cfrac{1}{3} \right )+\cfrac{5}{3}}{3k+4} = k + \cfrac{1}{3} \left( 1 + \cfrac{5}{3k+4} \right)[/imath] không phải số nguyên → không thỏa (C)
(3): [imath]\cfrac{3k^2+k+1}{3k+2} = \cfrac{(3k+2) \left ( k-\cfrac{1}{3} \right) + \cfrac{5}{3} }{3k+2} = k - \cfrac{1}{3} \left ( 1 - \cfrac{5}{3k + 2} \right )[/imath] nguyên khi k = 1 → (x, n, p) = (3, 2, 5)
→ (x, n, p) ∈ { (1, 1, 5), (3, 2, 5) }
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
