[tex]y'=(f'(x)-2).f''(f(x)-2x)[/tex]
Xét: [tex]y'=0 \Leftrightarrow \left[\begin{array}{l} f'(x)=2(1)\\f''(f(x)-2x)=0(2)\end{array}\right.[/tex]
$pt(1)$ có $3$ nghiệm phân biệt $\left[\begin{array}{l} x=u\\x=0\\x=t \end{array}\right.$ rồi nhé
Xét $pt(2):$
Có $f'(0)=2$ nên $ d=2$ ta sẽ có: $f(x)=ax^4 +bx^3+cx^2+2x+e$
Tiếp theo có tiếp: [tex]pt(2)\Leftrightarrow \left[\begin{array}{l} f(x)-2x=m\\f(x)-2x=n\end{array}\right.\\\Leftrightarrow \left[\begin{array}{l} ax^4+bx^3+cx^2=m-e(3)\\ax^4+bx^3+cx^2=n-e(4)\end{array}\right.[/tex]
Xét hàm $g(x)= ax^4+bx^3+cx^2\\g'(x)=4ax^3+3bx^2+2cx$
Xét $g'(x)=0 \Leftrightarrow 4ax^3+3bx^2+2cx+2=2 \\ \Leftrightarrow f'(x)=2 \Leftrightarrow \left[\begin{array}{l} x=u\\x=0\\x=t \end{array}\right.$
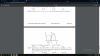
BBT của $g(x)$:
\begin{array}{c|ccccccccc}
x & -\infty & & u & & 0 & & t & & +\infty \\
\hline
y' & & + & 0 & - & 0 & + & 0 & - \\
\hline
& & & g(u) & & & & g(t) & & \\
& & \nearrow & & \searrow & & \nearrow & & \searrow & \\
y & -\infty & & & & 0 & & & & -\infty
\end{array}
Do $e>n$ nên $m-e<0$ và $n-e<0$
Do đó phương trình $(3)$ và $(4)$ mỗi phương trình có $2$ nghiệm không trùng nhau và tất nhiên không trùng với $3$ nghiệm của $pt(1)$
Như vậy $y'=0$ có 7 nghiệm đơn nên hàm có 7 cực trị
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
