[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
HỆ THỨC LƯỢNG TRONG TAM GIÁC
1. Định lí côsin

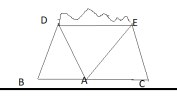
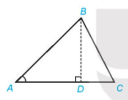
Chứng minh định lí
[imath]\cos \alpha=\dfrac{AD}{c}\Rightarrow AD=c\cos \alpha[/imath]
[imath]a^2=BD^2+CD^2=c^2-AD^2+(AD+b)^2=c^2+2AD.b+b^2[/imath]
[imath]=c^2+2cb\cos \alpha+b^2=c^2-2cb\cos A+b^2[/imath]
Người ta cũng CM đối với cả trường hợp góc A là góc vuông hoặc nhọn (Các bạn đọc có thể tự CM)
Định lí côsin. Trong tam giác ABC:
[imath]a^2=b^2+c^2-2bc\cos A[/imath]
[imath]b^2=c^2+a^2-2ca\cos B[/imath]
[imath]c^2=a^2+b^2-2ab\cos C[/imath]
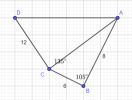
Luyện tập 1. Cho tam giác [imath]ABC[/imath] có [imath]AB=5, AC=8[/imath] và [imath]\widehat{A}=45^\circ[/imath]. Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.[imath]b^2=c^2+a^2-2ca\cos B[/imath]
[imath]c^2=a^2+b^2-2ab\cos C[/imath]
Áp dụng định lí coossin cho tam giác ABC, ta có:
[imath]BC^2=AB^2+AC^2-2AB.AC\cos \widehat{A}=89-40\sqrt2\Rightarrow BC=\sqrt{89-40\sqrt2}[/imath]
[imath]\cos \widehat{B}=\dfrac{AB^2+BC^2-AC^2}{2AB.BC}=\dfrac{50-40\sqrt2}{10(89-40\sqrt2)}\Rightarrow \widehat{B}\approx 91.16^\circ[/imath]
[imath]\Rightarrow \widehat{C}=180^\circ-\widehat{A}-\widehat{B}=43.84^\circ[/imath]
2. Định lí sin
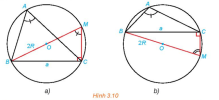
Chứng minh định lí a) trong trường hợp tam giác ABC nhọn, b) trong trường hợp tam giác ABC tù
a) Xét [imath]\Delta CBM[/imath] vuông tại C có [imath]\sin \widehat{BMC}=\dfrac{BC}{BM}=\dfrac{a}{2R}[/imath]
Mà [imath]\widehat{BMC}=\widehat{BAC}[/imath]
Suy ra [imath]\dfrac{a}{\sin \widehat{BAC}}=2R[/imath]
b) Xét [imath]\Delta CBM[/imath] vuông tại C có [imath]\sin \widehat{BMC}=\dfrac{BC}{BM}=\dfrac{a}{2R}[/imath]
[imath]\widehat{BAC}[/imath] chắn cung lớn BC; [imath]\widehat{BMC}[/imath] chắn cung bé BC
[imath]\Rightarrow \widehat{BAC}+ \widehat{BMC}=180^\circ\Rightarrow \sin \widehat{BAC}=\sin \widehat{BMC}[/imath]
Suy ra [imath]\dfrac{a}{\sin \widehat{BAC}}=2R[/imath]
Định lí sin. Trong tam giác ABC: [imath]\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin c}=2R[/imath]
Luyện tập 2. Cho tam giác ABC có [imath]b=8,c=5[/imath] và [imath]\widehat{B}=80^\circ[/imath]. Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.
Áp dụng định lí sin cho tam giác ABC có
[imath]R=\dfrac{b}{2\sin \widehat{B}}\approx 4.06[/imath]
[imath]\dfrac{b}{\sin \widehat{B}}=\dfrac{c}{\sin \widehat{C}}\Rightarrow \sin \widehat{C}=\dfrac{c.\sin \widehat{B}}{b}\Rightarrow \widehat{C}\approx 38^\circ[/imath]
[imath]\Rightarrow \widehat{A}=180^\circ-\widehat{B}-\widehat{C}=62^\circ[/imath]
[imath]\dfrac{b}{\sin \widehat{B}}=\dfrac{a}{\sin \widehat{A}}\Rightarrow a=\dfrac{b\sin \widehat{A}}{\sin \widehat{B}}\approx 7.17[/imath]
 Hôm nay tạm đến đây thôi nhé
Hôm nay tạm đến đây thôi nhéHẹn gặp lại các bạn ở các bài tiếp theo nha




 Hehee hôm nay dừng lại tại đây nhé
Hehee hôm nay dừng lại tại đây nhé