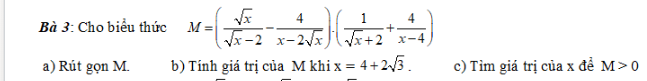a) [math]M=(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4}{\sqrt{x}(\sqrt{x}-2)}).(\dfrac{1}{\sqrt{x}+2}+\dfrac{4}{(\sqrt{x}+2)(\sqrt{x}-2)})[/math][math]=\dfrac{(\sqrt{x}+2)(\sqrt{x}-2)}{\sqrt{x}(\sqrt{x}-2)}.\dfrac{\sqrt{x}+2}{(\sqrt{x}+2)(\sqrt{x}-2)}=\dfrac{(\sqrt{x}+2)}{(\sqrt{x}-2)\sqrt{x}}[/math]b) [math]\sqrt{x}=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1[/math]Thay vào M :[imath]M=\dfrac{3+\sqrt{3}}{2}[/imath]
c)
Với x>0 ta có : [imath]\begin{cases} \sqrt{x}>0\\\sqrt{x}+2>0 \end{cases}[/imath]
nên để M >0 ta chỉ cần [imath]\sqrt{x}-2 >0 \Leftrightarrow \sqrt{x} >2 \Leftrightarrow x >4[/imath]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
