[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I.QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN TRONG MỘT TAM GIÁC
Kiến thức cần nhớ:
Định lý 1. Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
Định lý 2. Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Ví dụ minh họa:
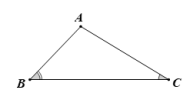
Nếu [imath]AC<AB[/imath] thì [imath]\widehat{B}<\widehat{C}[/imath] và ngược lại
II.QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU
Kiến thức cần nhớ:
Định lý 1. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Định lý 2. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
+ Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
+ Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
+ Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại, nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Ví dụ minh họa: Cho đề như hình vẽ khi đó:
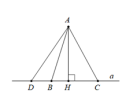
+, [imath]HD > HB[/imath] thì [imath]AD >AB[/imath] và ngược lại
+, Hoặc [imath]HD = HB[/imath] thì [imath]AD =AB[/imath]
III.QUAN HỆ GIỮA CẠNH CỦA MỘT TAM GIÁC. BẤT ĐẲNG THỨC TAM GIÁC.
Kiến thức cần nhớ:
Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hệ quả:Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.
Ví dụ minh họa:
Cho đề như hình vẽ thì [imath]|b-c|<a<b+c[/imath]
IV.TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC.
Kiến thức cần nhớ:
+ Đường trung tuyến của tam giác là đoạn thẳng nối đỉnh và trung điểm cạnh đối diện.
+ Mỗi tam giác có ba đường trung tuyến.
Định lý 1: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác đó.
Định lý 2: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng [imath]\dfrac{2}{3}[/imath] độ dài đường trung tuyến đi qua đỉnh ấy.
Ví dụ minh họa:
[imath]\dfrac{GA}{DA}=\dfrac{GB}{EB}=\dfrac{GC}{FC}=\dfrac{2}{3}[/imath]
V.TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA MỘT TAM GIÁC
Kiến thức cần nhớ:
Định lý 1: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến của tam giác đó
Định lí 2:Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó
Ví dụ minh họa: Do phần này khá dễ để hình dung nên mình sẽ không lấy ví dụ minh họa nhé ^^
VI.TÍNH CHẤT ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG
Kiến thức cần nhớ:
Định nghĩa :Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
Định lí 1:Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Định lý 2:Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Hệ quả: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Ví dụ minh họa :
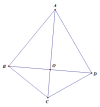
Cho đề như hình vẽ thì ta có:
+, AC là trung trực BD do đó [imath]OB=OD, AB=AD , BC=DC[/imath]
+, Nếu [imath]AB=AD[/imath] thì A nằm trên trung trực của BD
Kiến thức cần nhớ:
Định lý 1. Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.
Định lý 2. Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Ví dụ minh họa:
Nếu [imath]AC<AB[/imath] thì [imath]\widehat{B}<\widehat{C}[/imath] và ngược lại
II.QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU
Kiến thức cần nhớ:
Định lý 1. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Định lý 2. Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
+ Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
+ Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
+ Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại, nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Ví dụ minh họa: Cho đề như hình vẽ khi đó:
+, [imath]HD > HB[/imath] thì [imath]AD >AB[/imath] và ngược lại
+, Hoặc [imath]HD = HB[/imath] thì [imath]AD =AB[/imath]
III.QUAN HỆ GIỮA CẠNH CỦA MỘT TAM GIÁC. BẤT ĐẲNG THỨC TAM GIÁC.
Kiến thức cần nhớ:
Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Hệ quả:Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.
Ví dụ minh họa:
Cho đề như hình vẽ thì [imath]|b-c|<a<b+c[/imath]
IV.TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC.
Kiến thức cần nhớ:
+ Đường trung tuyến của tam giác là đoạn thẳng nối đỉnh và trung điểm cạnh đối diện.
+ Mỗi tam giác có ba đường trung tuyến.
Định lý 1: Ba đường trung tuyến của tam giác cùng đi qua một điểm. Điểm đó gọi là trọng tâm của tam giác đó.
Định lý 2: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng [imath]\dfrac{2}{3}[/imath] độ dài đường trung tuyến đi qua đỉnh ấy.
Ví dụ minh họa:
[imath]\dfrac{GA}{DA}=\dfrac{GB}{EB}=\dfrac{GC}{FC}=\dfrac{2}{3}[/imath]
V.TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA MỘT TAM GIÁC
Kiến thức cần nhớ:
Định lý 1: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến của tam giác đó
Định lí 2:Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó
Ví dụ minh họa: Do phần này khá dễ để hình dung nên mình sẽ không lấy ví dụ minh họa nhé ^^
VI.TÍNH CHẤT ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG
Kiến thức cần nhớ:
Định nghĩa :Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
Định lí 1:Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Định lý 2:Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Hệ quả: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Ví dụ minh họa :
Cho đề như hình vẽ thì ta có:
+, AC là trung trực BD do đó [imath]OB=OD, AB=AD , BC=DC[/imath]
+, Nếu [imath]AB=AD[/imath] thì A nằm trên trung trực của BD
