pp khảo sát sự biến thiên của hàm số chứa tham số m

[nguyenhoang140]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Các dạng toán về tính đơn điệu của hàm số

• DẠNG 1: Xét tính đồng biến nghịch biến của hàm số.

Phương pháp:
Xét tính đơn điệu của hàm số y=f(x) trên D ta thực hiện:

• Tìm miền xác định của hàm số.

• Tính đạo hàm f'(x) và giải phương trình f'(x)=0

• Lập bảng xét dấu f'(x) và kết luận về tính đồng biến nghịch biến của hàm số.

Các bài tập ví dụ:
Xét tính đồng biến nghịch biến của các hàm số:
y=x^3+9x^2+15x-3
y=(x+1)^1(2-x)
y=x^3-3x^2+3x=2
y=-x^3+2x^2-7x

• DẠNG 2: Tìm điều kiện để hàm số đơn điệu trên khoảng cho trước:
  Phương pháp:
  Muốn tìm điều kiện của tham số m để hàm số f(x,m) đơn điệu trên D, ta thực hiện:
  Tìm MXĐ của hàm số là Df. (D chứa trong Df)
  Tìm đạo hàm y’ của y.
  Tìm m để y’>=0 (hoặc y’ <=0) trên Df.
  Chú ý: Cần nắm vững và vận dụng các kết quả về định lý dấu tam thức bậc hai, các trường hợp so sánh một số α với nghiệm cảu tam thức:
  f(x)=ax2 + bx +c (a ≠ 0)
  1. điều kiện không đổi dấu của f(x):
  
  
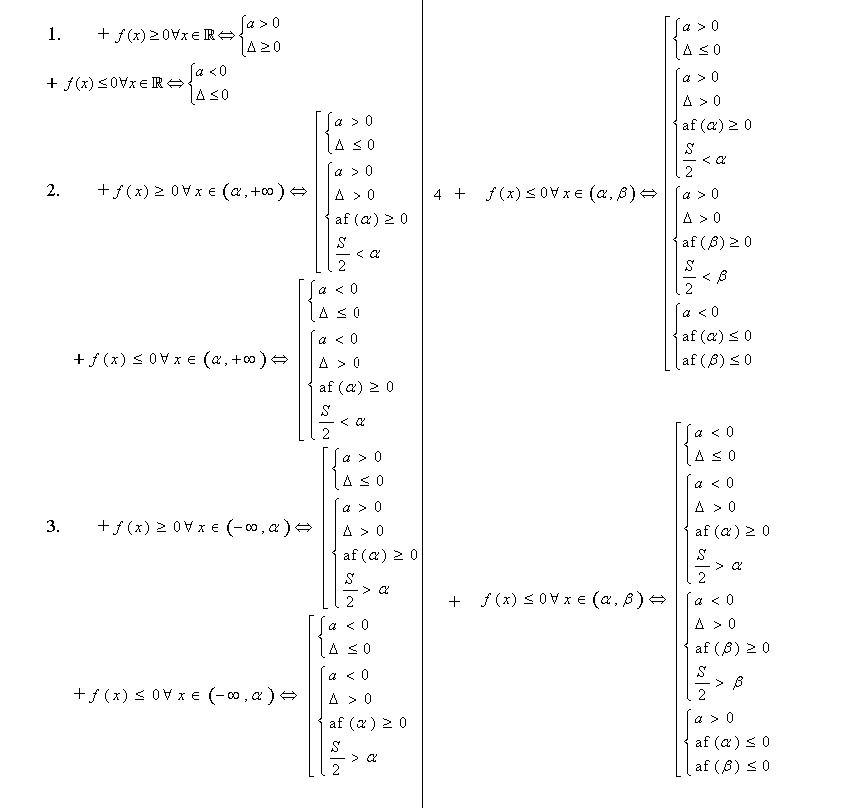
• Dạng 3: Sử dụng tính đơn điệu để chứng minh bất đẳng thức:
• Phương pháp:

- Chọn hàm số f(x) thích hợp.
- Xét tính đơn điệu của hàm số f(x) và áp dụng tính đơn điệu đó để suy ra BĐT cần chứng minh:
+ Nếu f(x) đồng biến trên [a,b] thì f(x)

f(a) hoặc f(x)

.
+ Nếu f(x) nghịch biến trên [a,b] thì f(x)

f(a) hoặc f(x)

f(b).


nguồn:http://www.thpt-phanboichau-daklak.edu.vn