B
bigbang195
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
MỘT SỐ VẤN ĐỀ CƠ SỞ VỀ PHƯƠNG TRÌNH NGHIỆm NGUYÊN
Trong chương trình toán THCS và THPT thì phương trình nghiệm nguyên vẫn luôn là một đề tài hay và khó đối với học sinh .
Các bài toán nghiệm nguyên thường xuyên có mặt tại các kì thi lớn , nhỏ , trong và ngoài nước .
Trong bài viết này tôi chỉ muốn đề cập đến các vấn đề cơ bản của nghiệm nguyên ( các dạng ; các phương pháp giải ) chứ không đi sâu ( vì vốn hiểu biết có hạn ). Tôi cũng sẽ không nói về phương trình Pell ( vì nó có nhiều trong các sách ) và phương trình Pythagore ; Fermat ( cũng có nhiều trong sách ; khái niệm rất đơn giản )
Chú ý : các bạn có thể tìm đọc thêm cuốn “ phương trình và bài toán nghiệm nguyên “ của thầy Vũ Hữu Bình .
Phương Pháp 1 Áp Dụng Tính Chia Hết
Dạng 1 :phương trình dạng
Ví dụ 1:: giải phương trình nghiệm nguyên sau :
Giải:
Có thể dễ dàng thấy
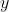chẵn . Đặt
.
Phương trình trở thành :
Từ đó ta có nghiệm phương trình này :
Chú ý : Ta còn có cách thứ
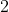để tìm nghiệm của phương trình trên . Đó là phương pháp tìm nghiệm riêng để giải phương trình bậc nhất
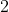ẩn
Ta dựa vào định lí sau :
Nếu phương trình
với
=1)
có
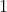tập nghiệm là
)
thì mọi nghiệm của phương trình nhận từ công thức
Định lí này chứng minh không khó ( bằng cách thế trực tiếp vào phương trình )
Dựa vào định lý này ; ta chỉ cần tìm
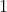nghiệm riêng của phương trình
.
Đối với các phương trình có hệ số
nhỏ thì việc tìm nghiệm khá đơn giản nhưng với các phương trình có
lớn thì không dễ dàng chút nào . Do đó ta phải dùng đến thuật toán ơ cơ lit ( các bạn có thể tìm đọc các sách ; tôi sẽ không nói nhiều về thuật toán này ) . Ngoài ra còn có thêm phương pháp hàm Euler .
Dạng 2 : Đưa về phương trình ước số :
Ví dụ 2: Giải phương trình nghiệm nguyên sau :
Giải :
 +5y=8)
 +5y]=24)
+15y=24)
+(2+3y).5 = 34)
(3y+2)=34)
Lập bảng dễ dàng tìm được nghiệm phương trình trên .
Ví dụ 3:Giải phương trình nghiệm nguyên sau :
Giải :
+2y^2-y+a=6+a)
là
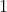số chưa biết ;
sẽ đc xác định sau .
Xét phương trình :
+2y^2-y+a=0)
^2-4(2y^2-y+a)=y^2-8y+4-4a)
Chọn
^2)
Từ đó ta có phương trình ước số :
(x+2y-3)=3)
Dạng 3:Phương pháp tách các giá trị nguyên
Ví dụ 4: Giải phương trình nghiệm nguyên sau :
Giải :
=y+2)
Phương Pháp 2 : Phương Pháp Lựa Chọn Modulo ( hay còn gọi là xét số dư từng vế )
Trước tiên ta có các tính chất cơ bản sau :
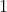số chính phương chia
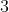dư
; chia
dư
; chia
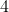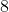dư
Ví Dụ 5 : Giải phương trình nghiệm nguyên sau :
Giải:
)
)
)
Còn
)
Do đó phương trình trên vô nghiệm.
Có thể mở rộng thêm cho nhiều modulo như
và mở rộng cho số lập phương ; tứ phương ; ngũ phương.......
Ta đến với Ví Dụ sau :
Ví dụ 6: Giải phương trình nghiệm nguyên dương sau :
Giải:
Dễ thấy
)
Mặt khác :
^x \equiv (-1)^x ( mod 5))
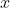chẵn thì
)
;
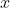lẻ thì
)
)
Còn
)
( vô lí)
Do đó phương trình trên vô nghiệm.
Chú ý : Nhiều bài toán nghiệm nguyên trong đề thi vô địch toán các nước đôi khi phải xét đến modulo khác lớn ; ta xét đến ví dụ sau :
Ví Dụ 7 :(Balkan1998) Giải phương trình nghiệm nguyên sau :
Giải:
)
)
( vô lí)
Do đó phương trình này vô nghiệm.
Chỉ
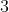dòng ; thật ngắn gọn và đẹp phải không nào.
Nói chung để xét modulo hiệu quả còn phải tùy thuộc vào sự nhạy bén của người làm toán.
Nói thêm :
Đối với các phương trình nghiệm nguyên có sự tham gia của các số lập phương thì modulo thường dùng là
vì
)
( hãy tự chứng minh )
Ta xét Ví Dụ sau .
Ví Dụ 8 : Giải phương trình nghiệm nguyên sau :
Dựa vào nhận xét trên :
)
Còn
)
( vô lí).
Do đó phương trình trên vô nghiệm
:khi (15)::khi (15)::khi (15)::khi (15)::khi (15):
Trong chương trình toán THCS và THPT thì phương trình nghiệm nguyên vẫn luôn là một đề tài hay và khó đối với học sinh .
Các bài toán nghiệm nguyên thường xuyên có mặt tại các kì thi lớn , nhỏ , trong và ngoài nước .
Trong bài viết này tôi chỉ muốn đề cập đến các vấn đề cơ bản của nghiệm nguyên ( các dạng ; các phương pháp giải ) chứ không đi sâu ( vì vốn hiểu biết có hạn ). Tôi cũng sẽ không nói về phương trình Pell ( vì nó có nhiều trong các sách ) và phương trình Pythagore ; Fermat ( cũng có nhiều trong sách ; khái niệm rất đơn giản )
Chú ý : các bạn có thể tìm đọc thêm cuốn “ phương trình và bài toán nghiệm nguyên “ của thầy Vũ Hữu Bình .
Phương Pháp 1 Áp Dụng Tính Chia Hết
Dạng 1 :phương trình dạng
Ví dụ 1:: giải phương trình nghiệm nguyên sau :
Giải:
Có thể dễ dàng thấy
Phương trình trở thành :
Từ đó ta có nghiệm phương trình này :
Chú ý : Ta còn có cách thứ
Ta dựa vào định lí sau :
Nếu phương trình
Định lí này chứng minh không khó ( bằng cách thế trực tiếp vào phương trình )
Dựa vào định lý này ; ta chỉ cần tìm
Đối với các phương trình có hệ số
Dạng 2 : Đưa về phương trình ước số :
Ví dụ 2: Giải phương trình nghiệm nguyên sau :
Giải :
Lập bảng dễ dàng tìm được nghiệm phương trình trên .
Ví dụ 3:Giải phương trình nghiệm nguyên sau :
Giải :
Xét phương trình :
Chọn
Từ đó ta có phương trình ước số :
Dạng 3:Phương pháp tách các giá trị nguyên
Ví dụ 4: Giải phương trình nghiệm nguyên sau :
Giải :
Phương Pháp 2 : Phương Pháp Lựa Chọn Modulo ( hay còn gọi là xét số dư từng vế )
Trước tiên ta có các tính chất cơ bản sau :
Ví Dụ 5 : Giải phương trình nghiệm nguyên sau :
Giải:
Còn
Do đó phương trình trên vô nghiệm.
Có thể mở rộng thêm cho nhiều modulo như
Ta đến với Ví Dụ sau :
Ví dụ 6: Giải phương trình nghiệm nguyên dương sau :
Giải:
Dễ thấy
Mặt khác :
Còn
Do đó phương trình trên vô nghiệm.
Chú ý : Nhiều bài toán nghiệm nguyên trong đề thi vô địch toán các nước đôi khi phải xét đến modulo khác lớn ; ta xét đến ví dụ sau :
Ví Dụ 7 :(Balkan1998) Giải phương trình nghiệm nguyên sau :
Giải:
Do đó phương trình này vô nghiệm.
Chỉ
Nói chung để xét modulo hiệu quả còn phải tùy thuộc vào sự nhạy bén của người làm toán.
Nói thêm :
Đối với các phương trình nghiệm nguyên có sự tham gia của các số lập phương thì modulo thường dùng là
Ta xét Ví Dụ sau .
Ví Dụ 8 : Giải phương trình nghiệm nguyên sau :
Dựa vào nhận xét trên :
Còn
Do đó phương trình trên vô nghiệm
:khi (15)::khi (15)::khi (15)::khi (15)::khi (15):