Gawr GuraĐặt [imath]cos 3x = t (|t| \leq 1)[/imath]
Khi đó PT trở thành : [imath]2t^2 + (3-2m)t + m-2 =0[/imath]
[math]\Delta = (2m-5)^2[/math]Nên PT có 2 nghiệm là :
[math]cox 3x = \dfrac{2m-3-(2m-5)}{4}= \dfrac{1}{2}[/math]và
[math]cox 3x = \dfrac{2m-3+(2m-5)}{4}= m -2 [/math]
• Xét TH1 : [imath]cox 3x = \dfrac{1}{2}[/imath]
Suy ra [imath]x = (+-) \dfrac{\pi}{9} + \dfrac{2}{3}k\pi[/imath]
Theo dữ kiện của đề bài thì các nghiệm thỏa mãn :
[math]x = \dfrac{\pi}{9}[/math]
[math]x = -\dfrac{\pi}{9}[/math]=> TH1 có 2 nghiệm
Do đó TH2 phải có 1 nghiệm
• Xét TH2: [imath]cox 3x = m-2[/imath]
[imath]x \in (\dfrac{-\pi}{6}; \dfrac{\pi}{3}) \rightarrow 3x \in (\dfrac{-\pi}{2}; \pi)[/imath]
Ta có bảng:
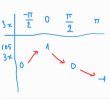
PT có 1 nghiệm nên : [imath]-1 \leq m -2 <0 0[/imath]
[imath]\iff 1 \leq m < 2[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.