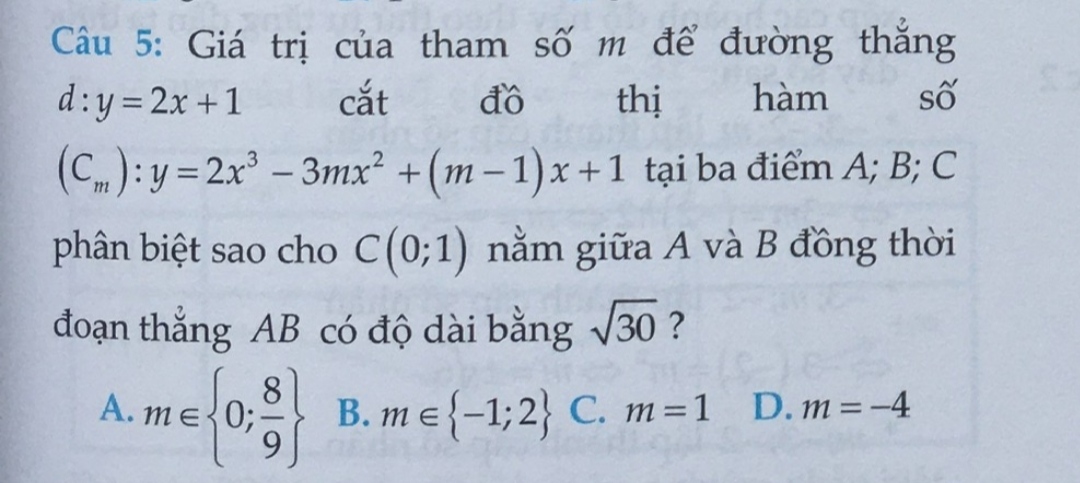Toán 12 Phương trình hoành độ giao điểm

[ntruc2319@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

 

[Tungtom]

Phương trình hoành độ giao điểm : $2x^3-3mx^2+(m-1)x+1=2x+1$
$<=>2x^3-3mx^2+x(m-3)=0$
$<=>x[2x^2-3mx+m-3]=0$.
Ycbt=> phương trình $2x^2-3mx+m-3$ có 2 nghiệm phân biệt thoả mãn $x_{A}<0<x_{B}=> x_{A}.x_{B}<0$.
Ta có: $\Delta= 9m^2-8m+24 >0$ với mọi $m$.
Theo định lí Vi-et:[tex]\left\{\begin{matrix} x_{A}+x_{B}=\frac{3m}{2} & \\ x_{A}.x_{B}=\frac{m-3}{2}& \end{matrix}\right.[/tex]
$x_{A}.x_{B}<0=> \frac{m-3}{2}<0=>m<3$
Lại có: $A=(x_{A};2x_{A}+1);B=(x_{B};2x_{B}+1)$
$=> (x_{B}-x_{A})^2+4(x_{B}-x_{A})^2=30$
$<=> (x_{B}-x_{A})^2=6$
$<=> (x_{B}+x_{A})^2-4x_{A}x_{B}=6$
$=>\frac{9}{4}m^2-2m=0$
$=>$ $m=0$(t/m) hoặc $m=\frac{8}{9}$ (t/m).
Em nghĩ là vậy ạ.