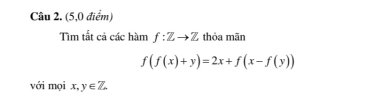Gọi [imath]P(x,y)[/imath] là phép thế cặp [imath](x,y)[/imath] vào giả thiết. Đặt [imath]a=f(0)[/imath]
[imath]P(0,0) \Rightarrow f(f(0))=f(-f(0)) \Rightarrow f(a)=f(-a)[/imath]
Ta sẽ chứng minh [imath]\exists m,n \in \mathbb{Z}[/imath] sao cho [imath]f(m)=-f(n)[/imath]
[imath]P(x,-f(x)) \Rightarrow f(0)=2x+f(x-f(-f(x))) \forall x \in \mathbb{Z}[/imath]
Nhận thấy tồn tại [imath]z,t \in \mathbb{Z}[/imath] sao cho [imath]f(0)-2z=-(f(0)-2t)[/imath]
Khi đó [imath]m=z-f(-f(z)), n=t-f(-f(t))[/imath] thỏa mãn.
[imath]P(x,a) \Rightarrow f(f(x)+a)=2x+f(x-f(a))[/imath]
[imath]P(x,-a) \Rightarrow f(f(x)-a)=2x+f(x-f(-a)) \Rightarrow f(f(x)-a)=f(f(x)+a)[/imath]
[imath]\Rightarrow f(f(m)-a)=f(f(m)+a)[/imath] (1)
[imath]P(a,x) \Rightarrow f(f(a)+x)=2a+f(a-f(x))[/imath]
[imath]P(-a,x) \Rightarrow f(f(-a)+x)=-2a+f(-a-f(x))[/imath]
[imath]\Rightarrow f(a-f(x))+2a=f(-a-f(x))-2a[/imath]
Thay [imath]x=n[/imath] vào ta có [imath]f(a-f(n))+2a=f(-a-f(n))-2a[/imath]
[imath]\Rightarrow f(a+f(m))+2a=f(-a+f(m))-2a[/imath] (2)
Kết hợp (1) với (2) ta được [imath]a=0[/imath] hay [imath]f(0)=0[/imath]
[imath]P(x,0) \Rightarrow f(f(x))=2x+f(x)[/imath]. Từ đó [imath]f[/imath] đơn ánh.
[imath]P(0,x) \Rightarrow f(x)=f(-f(x)) \Rightarrow x=-f(x) \Rightarrow f(x)=-x \forall x \in \mathbb{Z}[/imath]
Thử lại ta thấy thỏa mãn. Vậy [imath]f(x)=-x[/imath] là nghiệm hàm duy nhất.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
