Bài 5: Viết phương trình đường thẳng d đi qua M(4;-2) và cắt đường tròn: [tex]x^2+y^2-2x-4y-4=0[/tex] tại 2 điểm phân biệt A và B sao cho AB=4
$x^2+y^2-2x-4y-4=0$
$\Rightarrow (x-1)^2+(y-2)^2=9$
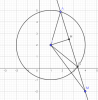
Gọi $I(1;2)$ là tâm đường tròn $(C), R=3$
Gọi $H$ là trung điểm $AB$
$IA=IB\Rightarrow \Delta AIB$ cân tại $I$
$\Rightarrow IH\bot AB$
$\Rightarrow IH=\sqrt{IB^2-HB^2}=\sqrt{IB^2-\dfrac{AB^2}{4}}=\sqrt5$
Gọi $H(a,b)$
$\vec{IH}=(a-1;b-2);\: \vec{MI}=(a-4;b+2)$
$\vec{IH}.\vec{HM}=0\Rightarrow (a-1)(a-4)+(b-2)(b+2)=0\Rightarrow a^2-5a+b^2=0\quad (1)$
$IH=\sqrt5\Rightarrow (a-1)^2+(b-2)^2=5\Rightarrow a^2-2a+b^2-4b=0\quad (2)$
(2)-(1)$\Rightarrow 3a=4b\Rightarrow b=\dfrac{3a}{4}$
Thay vào (1) ta có: $a^2-5a+\dfrac{9a^2}{16}=0\Leftrightarrow \left[\begin{matrix}a=0\\a=\dfrac{16}5\end{matrix}\right.$
Vậy $H(0;0)$ hoặc $H\left(\dfrac{16}{5};\dfrac{12}{5}\right)$
Từ đây em viết tiếp ptđt nhé
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em có thể tham khảo thêm các kiến thức tại:
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
