- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Lý thuyết
- trong mặt phẳng Oxy, cho điểm [tex]I(a;b)[/tex]. tập hơp các điểm M cách điểm I 1 khoảng cố định R là 1 đường tròn tâm I, bán kính R.
- phương trình đường tròn: [tex](x-a)^2+(y-b)^2=R^2[/tex]
* Nhận xét:
Phương trình đường tròn [tex](x-a)^2+(y-b)^2=R^2[/tex] thường được viết dưới dạng: [tex]x^2+y^2-2ax-2by+c=0[/tex] với [tex]c=a^2+b^2-R^2[/tex] hay [tex]R^2=a^2+b^2-c[/tex]
Ngược lại, phương trình [tex]x^2+y^2-2ax-2by+c=0[/tex] là phương trình của đường tròn (C) khi và chỉ khi
[tex]R^2=a^2+b^2-c>0[/tex]. khi đó đường tròn (C) có tâm I(a;b) và bán kính [tex]R=\sqrt{a^2+b^2-c}[/tex]
-Phương trình tiếp tuyến của đường tròn:
cho điểm [tex]M_0(x_0;y_0)[/tex] nằm trên đường tròn (C) tâm I(a;b). gọi d là tiếp tuyến của đường tròn tại điểm [tex]M_0[/tex].
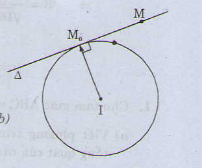
ta có [tex]M_0\in d[/tex] và vecto [tex]\overrightarrow{IM}(x_0-a;y_0-b)[/tex] là vecto pháp tuyến của đường thẳng d, do đó tiếp tuyến d có phương trình:
[tex](x_0-a).(x-x_0)+(y_0-b).(y-y_0)=0[/tex]
- tương giao với đường thẳng:
cho đường thẳng d và đường (C) tâm I(a;b), bán kính R. khoảng cách từ tâm đường tròn tới đường thẳng là h.
+ nếu h>R => đường tròn và đường thẳng không có điểm chung
+ nếu h=R => đường thẳng tiếp xúc với đường tròn tại tiếp điểm M. d là 1 tiếp tuyến của đường tròn (C).
+nếu h<R => đường thẳng cắt đường tròn tại 2 điểm A. B. độ dài dây cung AB: [tex]AB=2\sqrt{R^2-h^2}[/tex]. nếu h=0, thì AB là 1 đường kính của đường tròn.
- trong mặt phẳng Oxy, cho điểm [tex]I(a;b)[/tex]. tập hơp các điểm M cách điểm I 1 khoảng cố định R là 1 đường tròn tâm I, bán kính R.
- phương trình đường tròn: [tex](x-a)^2+(y-b)^2=R^2[/tex]
* Nhận xét:
Phương trình đường tròn [tex](x-a)^2+(y-b)^2=R^2[/tex] thường được viết dưới dạng: [tex]x^2+y^2-2ax-2by+c=0[/tex] với [tex]c=a^2+b^2-R^2[/tex] hay [tex]R^2=a^2+b^2-c[/tex]
Ngược lại, phương trình [tex]x^2+y^2-2ax-2by+c=0[/tex] là phương trình của đường tròn (C) khi và chỉ khi
[tex]R^2=a^2+b^2-c>0[/tex]. khi đó đường tròn (C) có tâm I(a;b) và bán kính [tex]R=\sqrt{a^2+b^2-c}[/tex]
-Phương trình tiếp tuyến của đường tròn:
cho điểm [tex]M_0(x_0;y_0)[/tex] nằm trên đường tròn (C) tâm I(a;b). gọi d là tiếp tuyến của đường tròn tại điểm [tex]M_0[/tex].
ta có [tex]M_0\in d[/tex] và vecto [tex]\overrightarrow{IM}(x_0-a;y_0-b)[/tex] là vecto pháp tuyến của đường thẳng d, do đó tiếp tuyến d có phương trình:
[tex](x_0-a).(x-x_0)+(y_0-b).(y-y_0)=0[/tex]
- tương giao với đường thẳng:
cho đường thẳng d và đường (C) tâm I(a;b), bán kính R. khoảng cách từ tâm đường tròn tới đường thẳng là h.
+ nếu h>R => đường tròn và đường thẳng không có điểm chung
+ nếu h=R => đường thẳng tiếp xúc với đường tròn tại tiếp điểm M. d là 1 tiếp tuyến của đường tròn (C).
+nếu h<R => đường thẳng cắt đường tròn tại 2 điểm A. B. độ dài dây cung AB: [tex]AB=2\sqrt{R^2-h^2}[/tex]. nếu h=0, thì AB là 1 đường kính của đường tròn.
