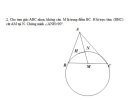
1. a) Nhận thấy [imath]E,F \in (AH)[/imath] và [imath]BEFC[/imath] nội tiếp nên [imath]AG,EF,BC[/imath] là [imath]3[/imath] trục đẳng phương của [imath](O),(AH),(BC)[/imath].
Từ đó [imath]AG,EF,BC[/imath] đồng quy tại [imath]R[/imath].
b) Vì [imath]P \in OM \Rightarrow MP \perp AG[/imath].
Mà [imath]PG[/imath] là tiếp tuyến của [imath](AH)[/imath] nên [imath]PA[/imath] cũng là tiếp tuyến [imath](AH)[/imath] hay [imath]PGMA[/imath] nội tiếp.
Lại có: [imath]NE,NF[/imath] là tiếp tuyến của [imath](AH)[/imath] nên [imath]\widehat{NFM}=\widehat{NEM}=\widehat{NDM}=90^o[/imath], suy ra [imath]M,F,D,N,E[/imath] đồng viên.
Ta thấy [imath](PGMA),(MBC),(MFDNE)[/imath] có chung điểm [imath]M[/imath].
Mặt khác, vì [imath]AG,EF,BC[/imath] là [imath]3[/imath] trục đẳng phương của [imath](O),(AH),(BC)[/imath] đồng quy tại [imath]R[/imath] nên [imath]RA \cdot RG=RE \cdot RF=RB \cdot RC[/imath].
Suy ra [imath]R[/imath] có cùng phương tích với [imath]3[/imath] đường tròn [imath](PGMA),(MBC),(MFDNE)[/imath].
Từ đó [imath](PGMA),(MBC),(MFDNE)[/imath] có trục đẳng phương chung là [imath]MR[/imath].
c) Vì [imath]T \in (PGMA), T \in (MFDNE)[/imath] nên [imath]\widehat{MTP}=\widehat{MTN}=90^o[/imath]
Từ đó [imath]P,T,N[/imath] thẳng hàng.
d) Ta sẽ chứng minh [imath]\widehat{GTN}=\widehat{GQN} \Leftrightarrow \widehat{PTG}=\widehat{AQG}[/imath]
Thật vậy, do [imath]\widehat{PTG}=\widehat{PMG}=\dfrac{1}{2}\widehat{AMG}=\widehat{AQG}[/imath] nên ta có điều phải chứng minh.
2. Đây được gọi là điểm Humpty nhé. Em có thể tìm kiếm tài liệu trên Internet để biết đầy đủ tính chất của điểm này.\
Ta định nghĩa lại điểm [imath]N[/imath] như sau: Gọi [imath]N[/imath] là hình chiếu của [imath]H[/imath] trên [imath]AM[/imath]. Ta sẽ chứng minh [imath]N \in (BHC)[/imath]
Vẽ đường kính [imath]AK[/imath] của [imath](O)[/imath]. [imath]KH[/imath] cắt [imath](O)[/imath] tại [imath]T \neq K[/imath]. Vẽ đường cao [imath]AD,BE,CF[/imath] của [imath]\Delta ABC[/imath].
Ta có kết quả quen thuộc là [imath]H,M,K[/imath] thẳng hàng. Mặt khác [imath]\widehat{ATH}=\widehat{ATK}=90^o[/imath] nên [imath]T \in (AH)[/imath]
Theo câu 1.a) thì ta có [imath]AT,EF,BC[/imath] đồng quy tại [imath]R[/imath].
Mặt khác, [imath]R[/imath] là giao điểm của [imath]EF[/imath] và [imath]BC[/imath] nên [imath](RD,BC)=-1 \Rightarrow RD \cdot RM=RB \cdot RC[/imath]
Lại có: [imath]AD \perp RM, MT \perp AR[/imath] nên [imath]H[/imath] là trực tâm của [imath]\Delta ARM[/imath] hay [imath]R,H,M[/imath] thẳng hàng.
Từ đó [imath]RH \cdot RM=RD \cdot RM=RB \cdot RC[/imath] hay [imath]BHNC[/imath] nội tiếp. Ta có điều phải chứng minh.
3. Nhận thấy [imath]QA^2=QB \cdot QC[/imath] nên [imath]Q[/imath] thuộc trục đẳng phương của [imath](A,0)[/imath] và [imath](M,ME)[/imath]
Mặt khác, [imath]\widehat{PAE}=\widehat{ACB}=\widehat{AFE} \Rightarrow \Delta PAE \sim \Delta PFA \Rightarrow PA^2=PE \cdot PF[/imath]
Từ đó [imath]P[/imath] thuộc trục đẳng phương của [imath](A,0)[/imath] và [imath](M,ME)[/imath]
Suy ra [imath]PQ \perp AM[/imath].
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé ^^ Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại đây nhé
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
