Toán 10 Phương tích - Trục đẳng phương

[kido2006]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

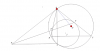
Cho tam giác $ABC$ nội tiếp $(O)$. $(J)$ là đường tròn tiếp xúc với $AB$; $AC$ tại $E$;$F$ và tiếp xúc
trong với $(O)$ tại $T$ (đường tròn A-mixtilinear nội tiếp của tam giác $ABC$). Tiếp tuyến tại $A$ của $(O)$
cắt $EF$ tại P. Chứng minh rằng [tex]\widehat{ATP} = 90[/tex]
Hình gửi kèm ạ :


Mọi người giúp em với ạ !!
@Mộc Nhãn

 

[7 1 2 5]

Gọi I là trung điểm EF. Theo định lí Lyness thì I là tâm đường tròn nội tiếp của tam giác ABC.
Ta có: [TEX]JE^2=JI.JA \Rightarrow JT^2=JI.JA \Rightarrow \Delta JTI \sim \Delta JAT \Rightarrow \widehat{JIT}=\widehat{JTA} \Rightarrow \widehat{TIP}=90^o-\widehat{JIT}=90^o-\widehat{JTA}=90^o-\widehat{OTA}=\widehat{ACT}=\widehat{PAT} \Rightarrow AITP[/TEX] nội tiếp
[TEX]\Rightarrow \widehat{ATP}=\widehat{AIP}=90^o[/TEX]