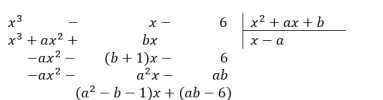Toán 8 Phép chia đa thức

[nguyenthiphuongmai2208]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho 2 đa thức [imath]f(x) = x^3 -x -6[/imath] và [imath]g(x) = x^2 +ax + b[/imath]. Xác định [imath]a[/imath] và [imath]b[/imath] để đa thức [imath]f(x)[/imath] chia hết cho đa thức [imath]g(x)[/imath]. Khi đó tìm đa thức thương
giúp e vs ạ sos

 

[Blue Plus]

Thực hiện phép chia

Đa thức [imath]f(x)[/imath] chia hết cho đa thức [imath]g(x)[/imath]
[imath]\Leftrightarrow (a^2-b-1)x+(ab-6)=0\forall x[/imath]
[imath]\Leftrightarrow \left\{\begin{matrix} a^2-b-1=0\\ab-6=0\end{matrix}\right.[/imath]
[imath]\Leftrightarrow \left\{\begin{matrix} b=a^2-1\\ab=6\end{matrix}\right.[/imath]
Thay [imath]b=a^2-1[/imath] ta có:
[imath]a(a^2-1)=6\\\Leftrightarrow a^3-a-6=0\\\Leftrightarrow a^3-2a^2+2a^2-4a+3a-6=0\\\Leftrightarrow a^2(a-2)+2a(a-2)+3(a-2)=0\\\Leftrightarrow (a-2)(a^2+2a+3)=0[/imath]
Vì [imath]a^2+2a+3=(a+1)^2+2>0[/imath] nên [imath]a=2[/imath]
Suy ra [imath]b=a^2-1=2^2-1=3[/imath]
Ta có đa thức thương là [imath]x-2[/imath]
Nếu có thắc mắc, bạn cứ hỏi tại đây, tụi mình sẽ hỗ trợ.
Ngoài ra bạn cũng có thể tham khảo Chuyên đề : Phân tích đa thức thành nhân tử