- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào các bạn, phần câu hỏi về cực trị gồm CĐ, CT và GTNN, GTLN cũng là 1 loại câu hỏi rất dễ xuất hiện trong câu hỏi về lí thuyết trong đề thi THPT QG sắp tới đây. Và mình thấy một số bạn còn nhầm lẫn giữa 2 loại khái niệm này. Nên hôm nay mình chia sẻ bài viết này để ai còn nhầm sẽ không bị nhầm nữa.
Mấy cái định nghĩa nhìn rối rối mắt thì có trong SGK hết rồi, nên mình sẽ không nhắc lai. CĐ, CT là điểm mà ở đó đồ thị hàm số có sự đảo chiều. Đồ thị đang đi lên xong đột nhiên cắm đầu xuống thì cho ta CĐ. Và ngược lại thì sẽ cho ta CT. Cho nên, nói đến CĐ, CT là các bạn cứ nghĩ đến ngay đạo hàm rồi giải pt đạo hàm = 0, ra nghiệm rồi lập BBT cho mình. Nhớ là nghiệm đơn nhé. Còn nghiệm kép ( kiểu biểu thức nghiệm có mũ chẵn:2,4,6......) thì ko phải cực trị, cái điều này chắc các bạn nghe nhiều rồi.
Còn GTLN, GTNN là giá trị lớn nhất/nhỏ nhất của hàm số trên toàn khoảng người ta đang yêu cầu xét, nó miễn quan tâm đồ thị hàm số có đảo chiều hay không. Vậy chắc các bạn cũng kết luận được trên 1 khoảng GTLN/GTNN thì chỉ có 1, còn cực trị thì có thể có nhiều phải không nào?
Cùng xem 1 số ví dụ sẽ sáng tỏ vấn đề.
Ví dụ 1:
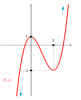
Đây là hình ảnh của đồ thị hàm số [tex]f(x)=x^3-3x^2+1[/tex]
Vậy nhận định về CT và GTLN/NN của hàm số này như thế nào?
Ta có :[tex]f'(x)=3x^2-6x;f'(x)=0 <=> x=0;x=2[/tex]
Và lập 0 và 2 sẽ là cực trị của hàm số rồi. Lập BBT hoặc nhìn trên đồ thị kia bạn sẽ thấy x=0 là điểm CĐ, x=2 là điểm CT của hàm số. Hàm số không có GTLN/NN vì rõ ràng xét trên R thì f(x) luôn tiến ra vô cùng khi x tiến ra vô cùng. Ta làm sao có thể tìm được điểm nào cao nhất/thấp nhất cho một thứ vô cùng. Đây cũng chính là đặc điểm chung của các hàm bậc 3, xét trên R nó không có GTLN/NN.
Vậy đổi khoảng đang xét 1 chút ta sẽ có ví dụ 2:
Đây cũng là đồ thị hàm số [tex]f(x)=x^3-3x^2+1[/tex] nhưng giờ người ta đổi khoảng xét trên [0;4] mà thôi.
Như vậy, rõ ràng ta thấy điểm f(2) nằm thấp nhất trên đoạn [0;4] nên tại x=2 hàm đạt GTNN / [0;4]. Đồng thời x=2 cũng là cực tiểu vì x=2 là nghiệm f'(x)=0.
Tại x=4 thì hàm đạt GTLN = 17. Rõ ràng trên [0;4] thì không có thằng nào >17 phải không.
Tại x=0 thì tuy cũng là nghiệm f'(x)=0, nhưng trên đoạn xét là [0;4] thì đó không phải điểm CĐ nữa. Theo định nghĩa của SGK thì cực trị là ta phải tìm được 1 khoảng (a;b) đủ nhỏ là tập con của tập [0;4] và chứa điểm x=0 đang xét. Nói nôm na dễ hiểu, các nhà toán học muốn tận mắt nhìn thấy đồ thị hàm số có sự đảo chiều tại điểm x=0 đó. Mặc dù chúng ta biết rõ nếu vẽ ra đoạn đồ thì về phần x<0 thì nó sẽ đảo chiều, nhưng họ cứ muốn phải thấy thì mới công nhận, kiểu trăm nghe không bằng một thấy vậy. Mà trên đoạn [0;4] , đồ thị chúng ta vẽ ra không thể show cho họ thấy điều đó. Cho nên rất tiếc phải chia buồn với anh bạn x=0 không được có 1 danh phận mang tên điểm cực đại, chỉ vì người ra đề keo kiệt cho cái khoảng bé tí đó là [0;4].
Vậy ta rút ra được kết luận gì:
1) Trên khoảng [a;b] thì tại cái đầu mút a;b không bao giờ có thể là cực trị. Nó chỉ có thể có khả năng là GTLN/NN mà thôi.
2) Điểm CĐ có thể đứng thấp hơn điểm CT. Điều này thể hiện rõ nét tại hàm phân thức rất hay gặp dạng bậc 2/ bậc 1.
Ví dụ: [tex]f(x)=\frac{x^2-x+2}{x+1}[/tex]
Đây là đồ thị của nó.
Bằng trực quan ta có thể thấy rõ ràng CĐ < CT nhưng nó vẫn đúng là CĐ, CT đó. Nên ai lập BBT mà gặp tình huống này thì đừng hoang mang gì cả. Chúc các bạn học tốt. Nếu ai có câu hỏi gì hãy comment xuống phía dưới!
@hip2608 @phuongthao1910@gmail.com
Mấy cái định nghĩa nhìn rối rối mắt thì có trong SGK hết rồi, nên mình sẽ không nhắc lai. CĐ, CT là điểm mà ở đó đồ thị hàm số có sự đảo chiều. Đồ thị đang đi lên xong đột nhiên cắm đầu xuống thì cho ta CĐ. Và ngược lại thì sẽ cho ta CT. Cho nên, nói đến CĐ, CT là các bạn cứ nghĩ đến ngay đạo hàm rồi giải pt đạo hàm = 0, ra nghiệm rồi lập BBT cho mình. Nhớ là nghiệm đơn nhé. Còn nghiệm kép ( kiểu biểu thức nghiệm có mũ chẵn:2,4,6......) thì ko phải cực trị, cái điều này chắc các bạn nghe nhiều rồi.
Còn GTLN, GTNN là giá trị lớn nhất/nhỏ nhất của hàm số trên toàn khoảng người ta đang yêu cầu xét, nó miễn quan tâm đồ thị hàm số có đảo chiều hay không. Vậy chắc các bạn cũng kết luận được trên 1 khoảng GTLN/GTNN thì chỉ có 1, còn cực trị thì có thể có nhiều phải không nào?
Cùng xem 1 số ví dụ sẽ sáng tỏ vấn đề.
Ví dụ 1:
Đây là hình ảnh của đồ thị hàm số [tex]f(x)=x^3-3x^2+1[/tex]
Vậy nhận định về CT và GTLN/NN của hàm số này như thế nào?
Ta có :[tex]f'(x)=3x^2-6x;f'(x)=0 <=> x=0;x=2[/tex]
Và lập 0 và 2 sẽ là cực trị của hàm số rồi. Lập BBT hoặc nhìn trên đồ thị kia bạn sẽ thấy x=0 là điểm CĐ, x=2 là điểm CT của hàm số. Hàm số không có GTLN/NN vì rõ ràng xét trên R thì f(x) luôn tiến ra vô cùng khi x tiến ra vô cùng. Ta làm sao có thể tìm được điểm nào cao nhất/thấp nhất cho một thứ vô cùng. Đây cũng chính là đặc điểm chung của các hàm bậc 3, xét trên R nó không có GTLN/NN.
Vậy đổi khoảng đang xét 1 chút ta sẽ có ví dụ 2:
Đây cũng là đồ thị hàm số [tex]f(x)=x^3-3x^2+1[/tex] nhưng giờ người ta đổi khoảng xét trên [0;4] mà thôi.
Như vậy, rõ ràng ta thấy điểm f(2) nằm thấp nhất trên đoạn [0;4] nên tại x=2 hàm đạt GTNN / [0;4]. Đồng thời x=2 cũng là cực tiểu vì x=2 là nghiệm f'(x)=0.
Tại x=4 thì hàm đạt GTLN = 17. Rõ ràng trên [0;4] thì không có thằng nào >17 phải không.
Tại x=0 thì tuy cũng là nghiệm f'(x)=0, nhưng trên đoạn xét là [0;4] thì đó không phải điểm CĐ nữa. Theo định nghĩa của SGK thì cực trị là ta phải tìm được 1 khoảng (a;b) đủ nhỏ là tập con của tập [0;4] và chứa điểm x=0 đang xét. Nói nôm na dễ hiểu, các nhà toán học muốn tận mắt nhìn thấy đồ thị hàm số có sự đảo chiều tại điểm x=0 đó. Mặc dù chúng ta biết rõ nếu vẽ ra đoạn đồ thì về phần x<0 thì nó sẽ đảo chiều, nhưng họ cứ muốn phải thấy thì mới công nhận, kiểu trăm nghe không bằng một thấy vậy. Mà trên đoạn [0;4] , đồ thị chúng ta vẽ ra không thể show cho họ thấy điều đó. Cho nên rất tiếc phải chia buồn với anh bạn x=0 không được có 1 danh phận mang tên điểm cực đại, chỉ vì người ra đề keo kiệt cho cái khoảng bé tí đó là [0;4].
Vậy ta rút ra được kết luận gì:
1) Trên khoảng [a;b] thì tại cái đầu mút a;b không bao giờ có thể là cực trị. Nó chỉ có thể có khả năng là GTLN/NN mà thôi.
2) Điểm CĐ có thể đứng thấp hơn điểm CT. Điều này thể hiện rõ nét tại hàm phân thức rất hay gặp dạng bậc 2/ bậc 1.
Ví dụ: [tex]f(x)=\frac{x^2-x+2}{x+1}[/tex]
Đây là đồ thị của nó.
Bằng trực quan ta có thể thấy rõ ràng CĐ < CT nhưng nó vẫn đúng là CĐ, CT đó. Nên ai lập BBT mà gặp tình huống này thì đừng hoang mang gì cả. Chúc các bạn học tốt. Nếu ai có câu hỏi gì hãy comment xuống phía dưới!
@hip2608 @phuongthao1910@gmail.com
