7.
[tex]y'=f'(x)-e^{-x} \\y'=0 \Leftrightarrow f'(x)=e^{-x}[/tex]
Ô vuông kia là R nhỉ, hàm f'(x) đồng biến trên R, hàm $g(x)=e^{-x}\\ \Rightarrow g'(x)=-e^{-x} <0 \forall x \in R$
Nên hàm $g(x)$ nghịch biến trên R
Vậy phương trình $f'(x)=e^{-x}$ có tối đa 1 nghiệm , nhận thấy $f'(0)=e^{-0}$ nên $x=0$ là nghiệm duy nhất của PT
Trục xét dấu của y'
Chọn B
8.
[tex]y'=4(m-1)x^2-4(m-3)x=0\\y'=0\Leftrightarrow \left[\begin{array}{l} x=0\\(m-1)x^2-4m+12=0(*) \end{array}\right.[/tex]
Với $m=1$ thì PT có nghiệm $x=0$ duy nhất, $y'$ đổi dấu từ $(-)$ sang $(+)$ nên $x=0$ là cực tiểu, nhận
Với $m \neq 1$ Để hàm không có cực đại thì PT $(*)$ phải vô nghiệm hoặc có nghiệm kép
Tương đương $\Delta \leq 0 \Leftrightarrow (m-1)(m-3) \leq 0 \Leftrightarrow 1 < m \leq 3 $
Vậy $1 \leq m \leq 3 $ thỏa đề
9.
[tex]f^2(x)f'(x)=xe^x\\\Leftrightarrow \int f^2(x)d(f(x))=\int xe^xdx\\\Leftrightarrow \frac{f^3(x)}{3}=(x-1)e^x+C[/tex]
$f(1)=1 \Rightarrow C=\frac{1 }{3}$
Suy được: $f(x)= \sqrt[3]{3(x-1)e^x+1}$
Giải PT $f(x)+1=0$ có:
$(x-1)e^x=\frac{-2}{3}$
KS hàm $g(x)=(x-1)e^x$ có:
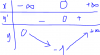
Vậy PT $f(x)+1=0$ có 2 nghiệm phân biệt
10.
PT tương đương [tex](\sqrt{2}+1)^{x^2-x+2}=\frac{1}{(\sqrt{2}+1)^{x^2-m}}\\\Leftrightarrow (\sqrt{2}+1)^{x^2-x+2}=(\sqrt{2}+1)^{m-x^2}\\\Leftrightarrow x^2-x+2=m-x^2[/tex]
Chọn luôn D vì hàm bậc 2 có tối đa 2 nghiệm
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
