- 1 Tháng mười hai 2017
- 446
- 283
- 89
- 23
- TP Hồ Chí Minh
- trường Quốc tế Á Châu
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
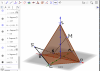
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trên các cạnh SD và AB lần lượt lấy các điểm M,N sao cho SD=3SM và AN=2NB.
a. Tìm giao tuyến của 2 mặt phăng (SAB) và (SCD).
b. Tìm giao điểm H của MN với mặt phẳng (SAC).
c. Chứng minh MN // (SBC).
d. Gọi (α) là mặt phẳng chứa MN và (α) // AD. Tìm thiết diện tạo bởi (α) và hình chóp.
Giúp mình với nhen, mình không giỏi Hình học cho lắm
a. Tìm giao tuyến của 2 mặt phăng (SAB) và (SCD).
b. Tìm giao điểm H của MN với mặt phẳng (SAC).
c. Chứng minh MN // (SBC).
d. Gọi (α) là mặt phẳng chứa MN và (α) // AD. Tìm thiết diện tạo bởi (α) và hình chóp.
Giúp mình với nhen, mình không giỏi Hình học cho lắm
Tình cảm là đôi giày, vừa chân ai nấy xỏ. Không phải của mình, đừng dòm ngó mất công.
Last edited: