- 9 Tháng tư 2020
- 1,049
- 1,064
- 181
- 20
- Hải Dương
- THPT Chuyên Nguyễn Trãi
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Hello mọi người!
Sắp thi học kì rồi nhỉ? Cùng ôn lại kiến thức về đường tròn nào!
Cùng ôn lại kiến thức về đường tròn nào!
I. Đường tròn
Đường tròn tâm O bán kính R là tập hợp các điểm cách đều điểm O một khoảng R.
Kí hiệu là (O;R).

Xét vị trí điểm A:
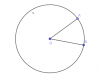
Đường kính là đường thẳng nối hai điểm phân biệt nằm trên đường tròn và đi qua tâm đường tròn đó.
Dây cung là đoạn thẳng nối hai điểm phân biệt nằm trên đường tròn và không đi qua tâm.

Trong đường tròn, đường kính vuông góc với một dây cung thì đi qua trung điểm của dây cung ấy.
Trong đường tròn, đường kính đi qua trung điểm của một dây cung không đi qua tâm thì vuông góc với dây cung ấy.
VD: [tex]OA\perp BC[/tex] tại D[tex]\Leftrightarrow[/tex] D là trung điểm BC.
III. Liên hệ giữa độ dài và khoảng cách đến tâm của dây cung.

Trong một đường tròn
IV. Vị trí tương đối của đường thẳng và đường tròn
Xét đường tròn bán kính R, d là khoảng cách từ đường thẳng đến tâm.
[TBODY]
[/TBODY]V. Góc trong đường tròn
VI. Tứ giác nội tiếp
1. Định nghĩa
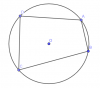
Một tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp)
2. Định lí
Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng [tex]180^{\circ}[/tex]
Xét tứ giác ABCD là tứ giác nội tiếp có: [tex]\widehat{ABC}=\widehat{ADC};\widehat{DAB}=\widehat{BCD}[/tex]
3. Định lí đảo
Nếu tứ giác có tổng số đo hai góc đối diện bằng [tex]180^{\circ}[/tex] thì tứ giác đó nội tiếp được đường tròn.
4. Dấu hiệu nhận biết
- Tứ giác có tổng hai góc đối bằng [tex]180^{\circ}[/tex]
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.
- Tứ giác có bốn đỉnh cách đều một điểm (mà có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc [tex]\alpha[/tex].
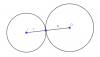
VII. Vị trí tương đối của hai đường tròn
Xét hai đường tròn (O;R) và (I;r), d là khoảng cách giữa hai tâm.
Chúc các bạn học tốt nha!
Tổng hợp topic ôn thi học kì

Sắp thi học kì rồi nhỉ?
 Cùng ôn lại kiến thức về đường tròn nào!
Cùng ôn lại kiến thức về đường tròn nào!
I. Đường tròn
Đường tròn tâm O bán kính R là tập hợp các điểm cách đều điểm O một khoảng R.
Kí hiệu là (O;R).
Xét vị trí điểm A:
- Nếu A nằm trên đường tròn (O; R) thì OA = R.
- Nếu A nằm trong đường tròn (O; R) thì OA < R.
- Nếu A nằm ngoài đường tròn (O; R) thì OA > R.
Đường kính là đường thẳng nối hai điểm phân biệt nằm trên đường tròn và đi qua tâm đường tròn đó.
Dây cung là đoạn thẳng nối hai điểm phân biệt nằm trên đường tròn và không đi qua tâm.
Trong đường tròn, đường kính vuông góc với một dây cung thì đi qua trung điểm của dây cung ấy.
Trong đường tròn, đường kính đi qua trung điểm của một dây cung không đi qua tâm thì vuông góc với dây cung ấy.
VD: [tex]OA\perp BC[/tex] tại D[tex]\Leftrightarrow[/tex] D là trung điểm BC.
III. Liên hệ giữa độ dài và khoảng cách đến tâm của dây cung.
Trong một đường tròn
- Khoảng cách đến tâm của hai dây cung bằng nhau [tex]\Leftrightarrow[/tex] hai dây cung bằng nhau.
- Khoảng cách đến tâm của một trong hai dây nhỏ hơn [tex]\Leftrightarrow[/tex] dây đó dài hơn.
IV. Vị trí tương đối của đường thẳng và đường tròn
Xét đường tròn bán kính R, d là khoảng cách từ đường thẳng đến tâm.
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức liên hệ d và R | Minh họa |
| Đường thẳng và đường tròn không giao nhau | 0 | d>R |
|
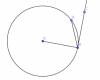
| Đường thẳng tiếp xúc với đường tròn⇔ tiếp tuyến | 1 | d=R |
|
| Đường thẳng cắt đường tròn ⇔ cát tuyến | 2 | d<R |
|

1. Định nghĩa
Một tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp)
2. Định lí
Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng [tex]180^{\circ}[/tex]
Xét tứ giác ABCD là tứ giác nội tiếp có: [tex]\widehat{ABC}=\widehat{ADC};\widehat{DAB}=\widehat{BCD}[/tex]
3. Định lí đảo
Nếu tứ giác có tổng số đo hai góc đối diện bằng [tex]180^{\circ}[/tex] thì tứ giác đó nội tiếp được đường tròn.
4. Dấu hiệu nhận biết
- Tứ giác có tổng hai góc đối bằng [tex]180^{\circ}[/tex]
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.
- Tứ giác có bốn đỉnh cách đều một điểm (mà có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc [tex]\alpha[/tex].
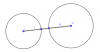
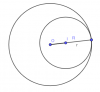
VII. Vị trí tương đối của hai đường tròn
Xét hai đường tròn (O;R) và (I;r), d là khoảng cách giữa hai tâm.

Tổng hợp topic ôn thi học kì