[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Xin chào mọi người, cũng sắp đến kì thi cuối HK1 rồi nên hôm nay mình sẽ tổng hợp kiến thức về Vectơ. Mong nó có thể giúp ích cho mọi người trong quá trình ôn thi 
Bài tổng hợp gồm có 3 phần :
+ Phần A: Lý thuyết
1. Định nghĩa
2. Tổng và hiệu hai vectơ
3. Tích của vectơ với một số
4. Hệ trục tọa độ
+ Phần B: Các dạng bài tập
+ Phần C: Ôn tập
Chúng ta cùng ôn tập nhé
A. Lý thuyết cần nhớ
I. Định nghĩa
1. Khái niệm vectơ
- Vectơ là một đoạn thẳng có hướng.
- Vectơ có điểm đầu là A, điểm cuối là B được kí hiệu là $\overrightarrow{AB}$ và đọc là “ vectơ $AB$ “.
- Vectơ không có điểm đầu vầ điểm cuối được kí hiệu $\vec{a}, \vec{b}, \vec{u},..$
2. Vectơ cùng phương và vectơ cùng hướng
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
- Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng.
3. Hai vectơ bằng nhau
- Độ dài vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.Kí hiệu: $\mid{\overrightarrow{AB}}\mid$
$\mid{\overrightarrow{AB}}\mid$ = $AB$
- Hai vectơ bằng nhau nếu chúng có cùng hướng và cùng độ dài.
Chú ý. Khi cho trước vectơ $\vec{a}$ và điểm O, thì ta luôn tìm được một điểm $A$ duy nhất sao cho $\overrightarrow{OA}=\vec{a}$
4. Vectơ - không
- Vectơ - không là vectơ có điểm đầu và điểm cuối trùng nhau. Kí hiệu: $\vec{0}$
$\overrightarrow{AA} = \overrightarrow{BB} = \overrightarrow{0}$
- Vectơ- không có độ dài bằng 0 và hướng tùy ý.
II. Tổng và hiệu hai vectơ
1. Tổng của hai vectơ
a) Định nghĩa:
Cho 2 vectơ $\vec{a}$ và $\vec{b}$. Lấy một điểm $A$ tùy ý, vẽ $\overrightarrow{AB}=\vec{a}$ và $\overrightarrow{BC}=\vec{b}$. Vectơ $\overrightarrow{AC}$ được gọi là tổng của 2 vectơ $\vec{a}$ và $\vec{b}$.
Kí hiệu : $\overrightarrow{AC}=\vec{a}+\vec{b}$
b) Quy tắc hình bình hành
Nếu $ABCD$ là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$
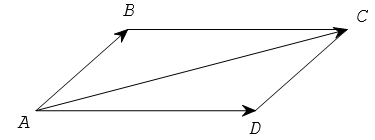
c) Tính chất của các phép cộng vectơ
- Tính chất giao hoán:
$\vec{a}+\vec{b}=\vec{b}+\vec{a}$
- Tính chất kết hợp:
$\big(\vec{a}+\vec{b}\big) + \vec{c} = \vec{a} + \big(\vec{b}+\vec{c}\big)$
- Tính chất của $\vec{0}$:
$\vec{a}+\vec{0}=\vec{0}+\vec{a}=\vec{a}$
2. Hiệu của hai vectơ
a) Vectơ đối:
Vectơ có cùng độ dài và ngược hướng với $\vec{a}$ được gọi là vectơ đối của vectơ $\vec{a}$. Kí hiệu: $-\vec{a}$
Vectơ đối của $\vec{0}$ là vectơ $\vec{0}$.
b) Hiệu của hai vectơ
Cho hai vectơ $\vec{a}$ và $\vec{b}$. Vectơ hiệu của hai vectơ $\vec{a}$ và $\vec{b}$ là vectơ $\vec{a}+\big(-\vec{b}\big)$. Kí hiệu: $\vec{a}-\vec{b}$
| $\vec{a}-\vec{b}=\vec{a}+\big(-\vec{b}\big)$ |
Với ba điểm $A, B, C$ bất kì, ta luôn có
$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ ( quy tắc 3 điểm )
$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ ( quy tắc trừ)
3. Áp dụng
a) Trung điểm của đoạn thẳng
$I$ là trung điểm $\Leftrightarrow \overrightarrow{IA}+\overrightarrow{IB}=\vec{0}$
b) Trọng tâm của tam giác
$G$ là trọng tâm của $\Delta ABC \Leftrightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$
III. Tích của vectơ với một số
1. Định nghĩa
Cho số $k \ne 0$ và $\vec{a} \ne \vec{0}$.Tích của một số $k$ với vectơ $\vec{a}$ là một vectơ. Kí hiệu: $k\vec{a}$
+ $k>0$: cùng hướng với vectơ $\vec{a}$
+ $k<0$: ngược hướng với vectơ $\vec{a}$
+ có độ dài bằng $\mid {k}\mid.\mid{\vec{a}}\mid$
Quy ước: $0.\vec{a} = 0, k.\vec{0} = \vec{0}$
2. Tính chất
Với hai vectơ $\vec{a}$ và $\vec{b}$ bất kì, vối mọi số $h$ và $k$, ta có:
+ $k.\big(\vec{a} + \vec{b}\big) = k\vec{a} + k\vec{b}$
+ $\big(h + k\big)\vec{a} = h\vec{a} + k\vec{b}$
+ $h\big(k\vec{a}\big) = \big(h.k)\vec{a}$
+ $1.\vec{a} = \vec{a} ; \big(-1)\vec{a} = -\vec{a}$
3. Trung điểm đoạn thẳng và trọng tâm của tam giác
+ Nếu $I$ là trung điểm của đoạn thẳng $AB$ thì với mọi điểm $M$, ta có:
| $\overrightarrow{MA}+\overrightarrow{MB} = 2\overrightarrow{MI}$ |
| $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} = 3\overrightarrow{MG}$ |
Điều kiện cần và đủ để hai vectơ $\vec{a}$ và $\vec{b} \big(\vec{b} \ne \vec{0}\big)$ cùng phương là có một số $k$ để $\vec{a} = k \vec{b}$
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có sô $k \ne 0$ để
$\vec{AB}= k \vec{AC}$
5. Phân tích một vectơ theo hai vectơ không cùng phương
Cho hai vectơ $\vec{a}$ và $\vec{b}$ không cùng phương. Khi đó mọi vectơ $\vec{x}$ đều phân tích được một cách duy nhất theo hai vectơ $\vec{a}$ và $\vec{b}$ nghĩa là có duy nhất cặp số $h, k$ sao cho $\vec{x} = h \vec{a} + k \vec{b}$
III. Hệ trục tọa độ
1. Trục và đội dài đại số trên trục
a) Trục tọa độ (hay gọi tắt là trục): là một đường thẳng trên đó đã xác định một điểm $O$ gọi là điểm gốc và một vectơ đơn vị $\vec{e}$
Ta kí hiệu trục đó là $(O ; \vec{e})$
b) Tọa độ của một điểm:
Ứng với M là một điểm tùy ý trên trục $\big(O,\vec{e}\big)$ thì có một số thực $k$ sao cho $\overrightarrow{OM} = k\vec{e}$
Ta gọi số k đó là tọa độ của điểm M đối với trục đã cho.
c) Độ dài đại số:
Cho hai điểm $A$ và $B$ trên trục $\overrightarrow{OM} = k\vec{e}$ . Khi đó tồn tại duy nhất số $a$ sao cho $\overrightarrow{AB} = a\vec{e}$
Ta gọi số $a$ là độ dài đại số của vectơ $\overrightarrow{AB}$ đối với trục đã cho và kí hiệu $a = \overrightarrow{AB}$
Nhận xét.
Nếu $ \overrightarrow{AB}$ cùng hướng với $\vec{e}$ thì $ \overrightarrow{AB}$ = AB, còn nếu $\overrightarrow{AB}$ ngược hướng với thì $= \overrightarrow{AB}= –AB $
Nếu hai điểm $A$ và $B$ trên trục $(O; \vec{e})$ có tọa độ lần lượt là $a$ và $b$ thì $\overrightarrow{AB} = b – a $.
2. Hệ trục tọa độ
a) Định nghĩa.
Hệ trục tọa độ $(O; \vec{i};\vec{j})$ gồm hai trục $(O;\vec{i})$ và $(O;\vec{j})$ vuông góc với nhau. Điểm gốc $O$ chung của hai trục gọi là gốc tọa độ. Trục $(O;\vec{i})$ được gọi là trục hoành và kí hiệu là $Ox$, trục $(O; \vec{j})$ được gọi là trục tung và kí hiệu là $Oy$. Các vectơ $\vec{i}$ và $\vec{j}$ là các vectơ đơn vị trên $Ox$ và $Oy$
$\mid\vec{i}\mid = \mid\vec{j}\mid = 1$
Hệ trục tọa độ $(O; \vec{i};\vec{j})$ còn được kí hiệu là $Oxy$
b) Tọa độ của vectơ
Trong mặt phẳng $Oxy$ cho một vectơ $\vec{u}$ tùy ý. Vẽ $\overrightarrow{OA} = \vec{u}$ và gọi $A_1, A_2$ lần lượt là hình chiếu của vuông góc của $A$ lên $Ox$ và $Oy$. Ta có $ \overrightarrow{OA} = \overrightarrow{OA_1} + \overrightarrow{OA_2}$ và cặp số duy nhất $(x; y)$ để $ \overrightarrow{OA_1}= x\vec{i} , \overrightarrow{OA_2} =y \vec{j}$.
Như vậy $\vec{u} = x \vec{i} +y \vec{j}$.
Cặp số $(x; y)$ duy nhất đó được gọi là tọa độ của vectơ $\vec{u}$ đối với hệ tọa độ $Oxy$ và viết $\vec{u} = (x; y)$ hoặc $\vec{u} (x; y)$. Số thứ nhất $x$ gọi là hoành độ, số thứ hai $y$ gọi là tung độ của vectơ
Như vậy
| $\vec{u} = (x; y) \Leftrightarrow \vec{u} = x \vec{i} +y \vec{j}$ |
Nếu $\vec{u} = (x; y)$ và $\vec{u’} = (x; y)$ thì
| $\vec{u} = \vec{u’} \Leftrightarrow \begin{cases} x=x’ \\ y =y’ \end{cases}$ |
Trong mặt phẳng tọa độ $Oxy$ cho một điểm $M$ tùy ý. Tọa độ của vectơ $\overrightarrow{OM}$ đối với hệ trục $Oxy$ được gọi là tọa độ của điểm $M$ đối với hệ trục đó.
Như vậy, cặp số $(x; y)$ là tọa độ của điểm $M$ khi và chỉ khi $\overrightarrow{OM}$ .Khi đó ta viết $M(x; y)$ hoặc $M = (x; y)$.
| $\overrightarrow{M} = (x; y) \Leftrightarrow \overrightarrow{OM} = x \vec{i} +y \vec{j}$ |
d) Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng
Cho hai điểm $A(x_A, y_A)$ và $B(x_B, y_B)$. Ta có
$\overrightarrow{AB} = ( x_B – x_A; y_B – y_A)$
3. Tọa độ của các vectơ
Cho $\vec{u} = (x_1; y_1), \vec{v} = (x_2, y_2)$
Khi đó
$\vec{u} + \vec{v} = (x_1 + x_2; y_1 + y_2)$
$\vec{u} - \vec{v} = (x_1 - x_2; y_1 - y_2)$
$k \vec{u} = (kx_1; ky_1)$
Nhận xét. Hai vectơ $\vec{u} = vec{u} = (x_1; y_1), \vec{v} = (x_2, y_2)$ với $\vec{v} \ne \vec{0}$ cùng phương khi và chỉ khi có một số $k$ sao cho \begin{cases}
x_1 = kx_2\\
y_1 = ky_2
\end{cases}.
4. Tọa độ trung điểm của đoạn thẳng. Tọa độ trọng tâm của tam giác
a) Cho đoạn thẳng $AB$ có $A(x_A, y_A), B(x_B, y_B)$. Ta dễ dàng chứng minh được tọa độ trung điểm $I(x_I, y_I)$ của đoạn thẳng $AB$ là
$x_I = \dfrac{x_A+x_B}{2}, y_I = \dfrac{y_A+y_B}{2}$
b) Cho tam giác $ABC$ có $A(x_A, y_A), B(x_B, y_B), C(x_C, y_C)$. Khi đó tọa độ của trọng tâm $G(x_G, y_G)$ của tam giác $ABC$ được tính theo công thức
$x_G = \dfrac{x_A + x_B + x_C}{3}, y_G = \dfrac{y_A + y_B + y_C}{3}$
B. Ôn tập
Dạng 1: Tìm tổng của hai hay nhiều vectơ.
Phương pháp giải:
Dùng định nghĩa tổng của hai vectơ, quy tắc ba điểm về tổng, quy tắc hình bình hành và các tính chất của tổng các vectơ.
Ví dụ minh họa:
Cho 5 điểm tùy ý $A, B, C, D, E$. Tính tổng .$ \overrightarrow{CD}+\overrightarrow{EC}+\overrightarrow{DA}+\overrightarrow{BE}$
Giải:
$ \overrightarrow{CD}+\overrightarrow{EC}+\overrightarrow{DA}+\overrightarrow{BE}$
.$=\big(\overrightarrow{CD}+\overrightarrow{EC}\big)+\big(\overrightarrow{DA}+\overrightarrow{BE}\big)$ (áp dụng tính chất giao hoán và kết hợp)
.$= \overrightarrow{CA}+\overrightarrow{BC}$(áp dụng quy tắc ba điểm)
.$=\overrightarrow{BC}+\overrightarrow{CA}$ (áp dụng tính chất giao hoán)
.$= \overrightarrow{BA}$ (áp dụng quy tắc ba điểm)
Dạng 2: Chứng minh đẳng thức vectơ.
Phương pháp giải: Sử dụng quy tắc ba điểm, quy tắc hình bình hành, trung điểm, trọng tâm, ….
Ví dụ minh họa:
Cho 4 điểm tùy ý $A, B, C, D$. Chứng minh đẳng thức sau:
$ \overrightarrow{AC}+\overrightarrow{BD}= \overrightarrow{AD}+\overrightarrow{BC}$
Giải:
+) Áp dụng quy tắc ba điểm ta có: $ \overrightarrow{AC} = \overrightarrow{AD}+\overrightarrow{DC}$
.
$\Rightarrow VT = \overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{BD}$
$\Rightarrow VT = \overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{DC}$
$\Rightarrow VT = \overrightarrow{AD}+\overrightarrow{BC}=VP$ (đpcm)
Dạng 3: Tính độ dài vectơ
Phương pháp giải:
Đưa tổng hoặc hiệu của các véctơ về một véctơ có độ dài là một cạnh của đa giác để tính độ dài của vectơ.
Ví dụ minh họa:
Cho hình chữ nhật $ABCD$. Biết $AB = 4a, AD = 2a$. Tính $ \mid\overrightarrow{AB}+\overrightarrow{AD}\mid$ .
Giải:
+) Áp dụng quy tắc hình bình hành ta có:
$\overrightarrow{AB}+\overrightarrow{AD} = \overrightarrow{AC}$
$ \Rightarrow \mid\overrightarrow{AB}+\overrightarrow{AD}\mid = \mid\overrightarrow{AC}\mid = AC $
+) Vì $ABCD$ là hình chữ nhật $BC = AD = 2a$.
+) Xét tam giác $ABC$ vuông tại $B$.
Áp dụng định lý Py-ta-go ta có:
$AC^2 = AB^2+ BC^2$
$\Rightarrow AC^2= (4a)^2+ (2a)^2= 20a^2 \Rightarrow AC = \sqrt{20a^2} = 2\sqrt{5}a$
$\Rightarrow \mid\overrightarrow{AB}+\overrightarrow{AD}\mid = \mid\overrightarrow{AC}\mid = AC = 2\sqrt{5}a$
Dạng 4: Chứng minh ba điểm thẳng hàng.
Phương pháp giải:
Ba điểm $A, B, C$ thẳng hàng $\Leftrightarrow\overrightarrow{AB} = k \overrightarrow{AC}$ . Áp dụng các quy tắc hình bình hành, quy tắc ba điểm, quy tắc trung điểm, quy tắc trọng tâm) hoặc xác định hai vectơ trên thông qua tổ hợp trung gian.
Ví dụ minh họa:
Cho 4 điểm $A, B, C, D$ sao cho . Chứng minh ba điểm $B, C, D$ thẳng hàng.
Giải:
$3\overrightarrow{AB}- 2\overrightarrow{AC}- \overrightarrow{AD} = \vec{0}$
$\Leftrightarrow 3\overrightarrow{AB}-2\big(\overrightarrow{AB}+\overrightarrow{BC}\big)- \big(\overrightarrow{AB}+\overrightarrow{BD}\big)=\vec{0} $
$\Leftrightarrow -2\overrightarrow{BC}- \overrightarrow{BD} = \vec{0}$
$\Leftrightarrow \overrightarrow{BD} =-2\overrightarrow{BC}$
Vậy $B, C, D$ thẳng hàng.
Dạng 5: Xác định tọa độ điểm, vectơ
Ví dụ minh họa:
Bài 1: Cho hai vectơ $\vec{u}= (3;-2)$ và $\vec{v}= (1;6)$ . Tính tọa độ các vectơ $\vec{u}+\vec{v}$ , $\vec{u}-\vec{v}$.
Giải:
+) Ta có: $\vec{u}+\vec{v}= (u_1 + v_1; u_2 + v_2) = ( 3 + 1 ; -2 + 6 ) = (4;4)$.
+) Ta có: $\vec{u}+\vec{v} = (u_1 – v_1; u_2 – v_2) = ( 3 - 1 ; -2 - 6 ) = (2;-8)$
C. Bài tập tự luyện
Bài 1: Cho hình chữ nhật $ABCD$. Chứng minh rằng . $ \overrightarrow{AB}+\overrightarrow{AD}= \overrightarrow{AB}+\overrightarrow{BC}$
Bài 2: Cho tam giác $ABC$ có $AM$ là trung tuyến. Gọi $I$ là trung điểm của $AM$ và $K$ là một điểm trên cạnh $AC$ sao cho $AK = \dfrac{1}{3}AC $ . Chứng minh ba điểm $B, I, K$ thẳng hàng.
Bài 3: Trong mặt phẳng $Oxy$, cho 3 điểm $A (-3;1), B (2;4)$ và $C (2;1)$. Tìm tọa độ trọng tâm $G$ của tam giác $ABC$, tọa độ trung điểm đoạn thẳng $AB, AC$.
Bài 4: Cho $A (1;2), B (-2;6)$. Điểm $M$ nằm trên trục $Oy$ sao cho ba điểm $A, B, M$ thẳng hàng. Tìm tọa độ điểm $M$
Bài 5: Cho các vectơ $\vec{a}= (4;-2), \vec{b}= (-1;-1)$ và $\vec{c}=(2;5) $. Phân tích vectơ $\vec{b}$ theo hai vectơ $\vec{a}$ và $\vec{c}$ .
Tổng hợp topic ôn thi học kì
Last edited by a moderator:
