[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Nhô nhô, mình lại tiếp tục làm phần ôn tập để hỗ trợ mọi người đây. Mong nó có thể giúp ích cho mọi người nheeee
. Cùng ôn tập thoiiii. Cố lên 
Bài này gồm có 3 phần nhe:
A. Lý thuyết
I. Giá trị lượng giác của một góc bất kì từ $0^o$ đến $180^o$
II. Tích vô hướng hai vectơ
III. Các hệ thức lượng trong tam giác
B. Các dạng bài tập
C. Ôn tập
A. Lý thuyết
I. Giá trị lượng giác của một góc bất kì từ $0^o$ đến $180^o$1. Định nghĩa
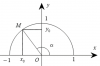
Với mỗi góc $\alpha (0^o \leq \alpha \leq 180^o)$ ta xác định một điểm $M$ trên nửa đường tròn đơn vị sao cho $\widehat{xOM} = \alpha$
Giả sử điểm $M$ có tọa độ $M(x_o, y_o)$.
Khi đó ta có:
$sin$ của góc $\alpha$ là $y_o$, kí hiệu $sin\alpha = y_o$
$cos$ của góc $\alpha$ là $x_o$, kí hiệu $cos\alpha = x_o$
$sin$ của góc $\alpha$ là $y_o$, kí hiệu $sin\alpha = y_o$
$tang$ của góc $\alpha$ là $\dfrac{y_o}{x_o}(x_o \ne 0)$ kí hiệu $tan\alpha = \dfrac{y_o}{x_o}$
$cotang$ của góc $\alpha$ là $\dfrac{x_o}{y_o}(y_o \ne 0)$ kí hiệu $cot\alpha = \dfrac{x_o}{y_o}$
2. Tính chất
Trên hình, ta có dây cung $NM$ song song với trục $Ox$ và nếu $\widehat{xOM} = \alpha$ thì $\widehat{xON} = 180^o- \alpha$. Ta có $y_M = y_N = y_o, x_M = –x_N = x_o$. Do đó
$sin\alpha = sin\big(180^o-\alpha\big) $
$cos\alpha = -cos\big(180^o-\alpha\big) $
$tan\alpha = -tan\big(180^o-\alpha\big) $
$cot\alpha = -cot\big(180^o-\alpha\big) $
3. Giá trị lượng giác của các góc đặc biệt
Trong bảng kí hiệu $“||”$ để chỉ giá trị lượng giác không xác định.
Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.
Chẳng hạn:
$sin120^o = sin\big(180^o-60^o \big)= sin60^o = \dfrac{\sqrt{3}}{2} $
$cos135^o = cos\big(180^o-45^o \big)=- cos45^o = -\dfrac{\sqrt{2}}{2} $
4. Góc giữa hai vectơ
a) Định nghĩa
Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác vectơ $\vec{0}$ .Từ một điểm $O$ bất kì ta vẽ $\overrightarrow{OA}=\vec{a}$ và $\overrightarrow{OB}=\vec{b}$. Góc $\widehat{AOB}$ với số đo từ $0^o$ đến $180^o$ được gọi là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$. Kí hiệu :$\big(\vec{a},\vec{b}\big)$
Nếu $\big(\vec{a},\vec{b}\big)= 90^o$ thì ta nói rằng $\vec{a}$ và $\vec{b}$ vuông góc với nhau, kí hiệu là $\vec{a} \bot \vec{b}$ hay $\vec{b} \bot \vec{a}$
b) Chú ý. Từ định nghĩa ta có $\big(\vec{a},\vec{b}\big)= \big(\vec{a},\vec{b}\big)$.
II. Tích vô hướng của hai vectơ
1. Định nghĩa
Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác vectơ $\vec{0}$ . Tích vô hướng của $\vec{a}$ và $\vec{b}$ là một số, kí hiệu là $\vec{a} . \vec{b}$ được xác định bởi công thức sau:
$\vec{a}.\vec{b}=\mid\vec{a}\mid . \mid\vec{b}\mid . cos\big(\vec{a},\vec{b}\big) $
Trường hợp ít nhất một trong hai vectơ $\vec{a}$ và $\vec{b}$ bằng vectơ $\vec{0}$ ta quy ước:
$\vec{a}.\vec{b}=0$
Chú ý
+) Với $\vec{a}$ và $\vec{b}$ khác vectơ $\vec{0}$ ta có:
$\vec{a}.\vec{b}=0 \Leftrightarrow \vec{a} \bot \vec{b} $
+) Khi $\vec{a}=\vec{b}$ tích vô hướng $\vec{a}.\vec{a}$ được kí hiệu là $\vec{a}^2$ ,được gọi là bình phương vô hướng của vectơ $\vec{a} $
Ta có:
$\vec{a}^2=\mid\vec{a}\mid . \mid\vec{a}\mid . cos0^o=\mid\vec{a}\mid^2$
2. Các tính chất của tích vô hướng
Với ba vectơ $\vec{a}, \vec{b}, \vec{c}$ bất kì và với mọi số $k$, ta có:
+ Tính chất giao hoán:
$\vec{a}.\vec{b} = \vec{b}.\vec{a}$
+ Tính chất phân phối:
$\vec{a}.\big(\vec{b}+\vec{c}\big) = \vec{a}.\vec{b}+\vec{a}.\vec{c}$
$\big(k\vec{a}\big).\vec{b} = k\big(\vec{a}.\vec{b}\big) = \vec{a}.\big(k\vec{b}\big)$
$\vec{a}^2 \geq 0, vec{a}^2 = 0 \Leftrightarrow vec{a}= 0$
Nhận xét:
Từ các tính chất, ta suy ra:
$\big(\vec{a}+\vec{b}\big)^2 =\vec{a}^2+2\vec{a}.\vec{b}+\vec{b}^2$
$\big(\vec{a}-\vec{b}\big)^2 =\vec{a}^2-2\vec{a}.\vec{b}+\vec{b}^2$
$\big(\vec{a}+\vec{b}\big)\big(\vec{a}-\vec{b}\big) =\vec{a}^2-\vec{b}^2$
3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ$\big(O; \vec{i}; \vec{j}\big)$, cho hai vectơ: $\vec{a}=\big(a_1, a_2\big), \vec{b}=\big(b_1, b_2\big)$
Khi đó tích vô hướng $\vec{a}.\vec{b}$
$\vec{a}.\vec{b} = a_1b_1+a_2b_2$
Nhận xét. Hai vectơ: $\vec{a}=\big(a_1, a_2\big), \vec{b}=\big(b_1, b_2\big)$ đều khác vectơ $\vec{0}$ vuông góc với nhau khi và chỉ khi: $a_1b_1 + a_2b_2 = 0$.
4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ $\vec{a}=\big(a_1, a_2\big)$được tính theo công thức:
$\mid\vec{a}\mid = \sqrt{a_1^2 + a_2^2}$
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu $\vec{a}=\big(a_1, a_2\big)$ và $\vec{b}=\big(b_1, b_2\big)$ đều khác $\vec{0}$ thì ta có:
$ cos\big(\vec{a},\vec{b}\big) = \dfrac{\vec{a}.\vec{b}}{\mid\vec{a}\mid . \mid\vec{b}\mid} = \dfrac{ a_1b_1 + a_2b_2}{\sqrt{a_1^2 + a_2^2}.\sqrt{b_1^2 + b_2^2}}$
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm $A(x_A; y_A)$ và $B(x_B; y_B)$ được tính theo công thức:
$AB = \sqrt{\big(x_B-x_A\big)^2 + \big(y_B-y_A\big)^2 }$
III. Các hệ thức lượng trong tam giác
1. Định lí côsin
Cho tam giác $ABC$ có $BC = a, AC = b$ và $AB = c$
Ta có
$a^2= b^2+ c^2 – 2bc.cosA$
$b^2 = c^2 + a^2 – 2ca.cosB$
$c^2 = a^2 + b^2 – 2ab.cosC$
Hệ quả:
$cosA = \dfrac{b^2 + c^2 - a^2}{2bc}; cosB = \dfrac{c^2 + a^2 - b^2}{2ca}; cosC = \dfrac{a^2 + b^2 - c^2}{2ab}$
2. Định lí sin
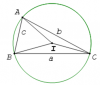
Cho tam giác $ABC$ có $BC = a, AC = b, AB = c$ và $R$ là bán kính đường tròn ngoại tiếp.
Ta có
$\dfrac{a}{sinA} = \dfrac{b}{sinB} = \dfrac{c}{sinC} = 2R$
3. Độ dài đường trung tuyến
Cho tam giác $ABC$ có $m_a, m_b, m_c$ lần lượt là các trung tuyến kẻ từ $A, B, C$.
Ta có
$m_a^2 = \dfrac{b^2 + c^2}{2} - \dfrac{a^2}{4}$
$m_b^2 = \dfrac{a^2 + c^2}{2} - \dfrac{b^2}{4}$
$m_c^2 = \dfrac{a^2 + b^2}{2} - \dfrac{c^2}{4}$
4. Công thức tính diện tích tam giác
Cho tam giác $ABC$ có
+) $h_a, h_b, h_c$ là độ dài đường cao lần lượt tương ứng với các cạnh $BC, CA, AB$
+) $R$ là bán kính đường tròn ngoại tiếp tam giác
+) $r$ là bán kính đường tròn nội tiếp tam giác
+) $p = \dfrac{a + b + b}{2}$ là nửa chu vi tam giác;
+) $S$ là diện tích tam giác.
Khi đó ta có:
$S = \dfrac{1}{2}a.h_a = \dfrac{1}{2}b.h_b = \dfrac{1}{2}c.h_c$
$= \dfrac{1}{2}bc.sinA = \dfrac{1}{2}ca.sinB = \dfrac{1}{2}ab.sinC$
$= \dfrac{abc}{4R}$
$=p.r$
$=\sqrt{p\big(p-a\big) \big(p-b\big) \big(p-c\big)}$
B. Các dạng bài tập
Dạng 1: Tính góc giữa hai vecto1. Phương pháp giải
Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ
Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính $cos$ góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ.
Sử dụng công thức sau:
$ cos\big(\vec{a},\vec{b}\big) = \dfrac{\vec{a}.\vec{b}}{\mid\vec{a}\mid . \mid\vec{b}\mid} = \dfrac{ a_1b_1 + a_2b_2}{\sqrt{a_1^2 + a_2^2}.\sqrt{b_1^2 + b_2^2}}, \big(\vec{a} \ne \vec{0}, \vec{b} \ne \vec{0}\big)$
Chú ý: Góc giữa hai vectơ thuộc $[0^o;180^o]$
2. Ví dụ minh họa
Ví dụ 1: Cho tam giác $ABC$ vuông cân tại $A$. Tính góc giữa hai vectơ: $\overrightarrow{BA}$ và $\overrightarrow{BC}$
Hướng dẫn giải:
a) $\big(\overrightarrow{BA}; \overrightarrow{BC}\big) =\widehat{ABC}$
Do $\Delta ABC$ vuông cân tại $A$ nên:
$\widehat{ABC} = \dfrac{180^o – 90^o}{2} = 45^o$
Vậy $\big(\overrightarrow{BA}; \overrightarrow{BC}\big) =\widehat{ABC} = 45^o$
Ví dụ 2: Cho các vectơ $\vec{a}=\big(-1;1\big), \vec{b}=\big(1;3\big)$ Tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$.
Hướng dẫn giải:
$ cos\big(\vec{a},\vec{b}\big) = \dfrac{\vec{a}.\vec{b}}{\mid\vec{a}\mid . \mid\vec{b}\mid} = \dfrac{ -1.1 + 1.3}{\sqrt{(-1)^2 + 1^2}.\sqrt{1^2 + 3^2}}$
Vậy góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ là góc $\alpha \in [0^o;180^o]$ thỏa mãn $cos\alpha = \dfrac{\sqrt{5}}{5}$.
Dạng 2: Tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ
1. Phương pháp giải
Độ dài vecto
- Phương pháp: muốn tính độ dài vectơ, ta tính độ dài cách giữa điểm đầu và điểm cuối của vectơ.
Khoảng cách giữa hai điểm trong hệ tọa độ
Áp dụng công thức sau
Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm $M(x_M, y_M)$ và $N(x_N, y_N)$ là
$MN = \mid MN \mid = \sqrt{\big(x_N-x_M\big)^2+\big(y_N-y_M\big)^2}$
2. Ví dụ minh họa
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{u}=\big(4;1\big)$ và $\vec{v}=\big(1;4\big)$. Tính độ dài vectơ $\vec{u}+\vec{v}, \vec{u} - \vec{v}$
Hướng dẫn giải:
Ta có:
$\vec{u}+\vec{v} = \big(4+1; 1+4\big) = \big(5;5\big)$
$\Rightarrow \mid\vec{u}+\vec{v}\mid = \sqrt{5^2+5^2} = \sqrt{50} = 5\sqrt{2}$
$\vec{u}-\vec{v} = \big(4-1; 1-4\big) = \big(3;-3\big)$
$\Rightarrow \mid\vec{u}-\vec{v}\mid = \sqrt{3^2+(-3)^2} = \sqrt{18} = 3\sqrt{2}$
Ví dụ 2: Trong mặt phẳng tọa độ $Oxy$, tính khoảng cách giữa hai điểm $M(1; -2)$ và $N (-3; 4)$.
Hướng dẫn giải:
$MN = \mid MN \mid = \sqrt{\big(x_N-x_M\big)^2 + \big(y_N-y_M\big)^2}$
$= \sqrt{\big(-3-1\big)^2+\big(4-(-2)\big)^2} = \sqrt{52} = 2\sqrt{13}$
Dạng 3: Chứng minh hai vecto vuông góc
1. Phương pháp giải
Phương pháp 1: Sử dụng định nghĩa
Nếu $\big(\vec{a},\vec{b}\big)= 90^o$ thì hai vectơ $\vec{a}$ và $\vec{b}$ vuông góc với nhau, kí hiệu $\vec{a} \bot \vec{b}$.
Phương pháp 2: Sử dụng tính chất của tích vô hướng và áp dụng trong hệ tọa độ
Cho $\vec{a} =(x;y)$ và $\vec{b} =(x’;y’)$
Khi đó:
$\vec{a} \bot \vec{b} \Leftrightarrow \vec{a}.\vec{b} = 0 \Leftrightarrow xx’ + yy’ = 0$
2. Ví dụ minh họa
Ví dụ 1: Cho hai vectơ $\vec{a}$ và $\vec{b}$ vuông góc với nhau và$\mid\vec{a}\mid = 1; \mid\vec{b}\mid = \sqrt{2}$ . Chứng minh hai vectơ $2\vec{a}-\vec{b}$ và $\vec{a} + \vec{b}$ vuông góc với nhau.
Hướng dẫn giải:
Do $\vec{a} \bot \vec{b} \Rightarrow \vec{a}.\vec{b}=0 $
Ta có:
$\big(2\vec{a}-\vec{b}\big). \big(\vec{a} + \vec{b}\big) = 2\vec{a}^2 + 2\vec{a}.\vec{b} - \vec{a}.\vec{b} - \vec{b}^2$
$=2\vec{a}^2 + \vec{a}.\vec{b} - \vec{b}^2$
$=2\mid\vec{a}\mid^2 + \vec{a}.\vec{b} - \mid\vec{b}\mid^2$
$=2.1^2 + 0 – \big(\sqrt{2}\big)^2 = 0$
Dạng 4: Tính cạnh/góc của tam giác
1. Phương pháp giải
+ Sử dụng định lý sin:
Cho tam giác $ABC$ có $BC = a, CA = b, AB = c$ và có $R$ bán kính đường tròn ngoại tiếp tam giác $ABC$
Khi đó ta có:
$\dfrac{a}{sinA} = \dfrac{b}{sinB} = \dfrac{c}{sinC} = 2R$
+ Sử dụng định lý Cô-sin:
Cho tam giác $ABC$ có $BC = a, AC = b$ và $AB = c$
Ta có
$a^2= b^2+ c^2 – 2bc.cosA$
$b^2 = c^2 + a^2 – 2ca.cosB$
$c^2 = a^2 + b^2 – 2ab.cosC$
Dạng 5: Tính diện tích tam giác
1. Phương pháp giải
Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức tính diện tích
2. Ví dụ minh họa
Ví dụ 1: Cho tam giác $ABC$ có $AC = 3, AB = 5, cosA = \dfrac{4}{5}$.
a, Tính diện tích tam giác $ABC$.
b, Tính đường cao $h_a$ của tam giác $ABC$.
Hướng dẫn giải:
a) Ta có: $sin^2A + cos^2A =1$
Suy ra $ sin^2A = 1-cos^2A = 1-\bigg(\dfrac{4}{5}\bigg)^2 = \dfrac{9}{25}$
$\Rightarrow sinA = \dfrac{3}{5}$
Áp dụng công thức tính diện tích tam giác, ta có diện tích tam giác $ABC$ là:
$S=\dfrac{1}{2}AB.AC.sinA=\dfrac{1}{2}.5.3. \dfrac{3}{5}=\dfrac{9}{2}$
b) Áp dụng định lý Cô-sin trong tam giác $ABC$, ta có”
$BC^2 = AB^2 + AC^2 -2.AB.AC.cosA$
$= 5^2 + 3^2 -2.5.3.\dfrac{4}{5}$
$=10$
Suy ra $BC =\sqrt{10}$
Áp dụng công thức tính diện tích tam giác $ABC$ ta lại có:
$S=\dfrac{1}{2}h_a.BC=\dfrac{9}{2}$
$\Leftrightarrow h_a.BC=9 \Leftrightarrow h_a = \dfrac{9}{BC} = \dfrac{9}{\sqrt{10}}$
Ví dụ 2: Cho tam giác $ABC$ có$\hat{B} =35^o, \hat{C}=50^o$ và cạnh $AC = 15$ cm. Tính các cạnh còn lại của tam giác $ABC$.
Hướng dẫn giải:
Ta có:
$\hat{A}+\hat{B}+\hat{C}=180^o \Rightarrow \hat{A} = 180^o - \hat{B} -\hat{C}= 180^o – 35^o - 50^o = 95^o$
Áp dụng định lý sin trong tam giác$ABC$ ta có:
$\dfrac{BC}{sinA} = \dfrac{AC}{sinB} = \dfrac{AB}{sinC}$
Suy ra: $\begin{cases}
BC=\dfrac{AC.sinA}{sinB}=\dfrac{15.sin95^o}{sin35^o} \approx20.05 cm \\
AB=\dfrac{AC.sinC}{sinB}=\dfrac{15.sin50^o}{sin35^o} \approx20.03 cm
\end{cases}$
Vậy $BC= 20,05 cm$ và $AB=20,03 cm$
C. Ôn Tập
Bài 1: Cho tam giác $ABC$ có$\hat{A}=60^o, AB=6, AC=8$ . Tính $BC$.Bài 2: Cho tam giác $ABC$ có cách cạnh $BC=6, CA =4\sqrt{2}, AB=2$.. Tính $cosA$ và góc $A$.
Bài 3: Cho tam giác $\hat{A}=75^o, \hat{B}=45^o $. Tính tỉ số $\dfrac{AB}{AC}$
Bài 4: Cho tam giác $ABC$ có các đỉnh $A(1; -2), B(-2; 3), C(0; 4)$. Tính diện tích tam giác $ABC$.
Tổng hợp topic ôn thi học kì
