[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
TAM GIÁC ĐỒNG DẠNG
1. ĐỊNH NGHĨA, QUY ƯỚC, KIẾN THỨC CẦN NHỚ
- Tỉ số 2 đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo (nhưng kết quả tính ra không chưa đơn vị đo)- Tỉ số của 2 đoạn thẳng AB và CD, được kí hiệu là [imath]\dfrac{AB}{CD}[/imath]
- Hai đoạn thẳng AB và CD gọi là tỉ lệ với 2 đoạn XY và ZT nếu có tỉ lệ thức [imath]\dfrac{AB}{CD} = \dfrac{XY}{ZT}[/imath]
- Kiến thức về tỉ lệ thức, dãy tỉ số bằng nhau.
2. ĐỊNH LÝ TALET TRONG TAM GIÁC
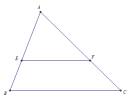
a) Định lý Talet
* Phát biểu: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
* Xét tam giác ABC có: [imath]EF // BC (E\in AB; F\in AC)[/imath]
Theo định lý Talet, ta có: [imath]\dfrac{AE}{AB} = \dfrac{AF}{AC}[/imath] hay [imath]\dfrac{AE}{EB} = \dfrac{AF}{FC}[/imath] hay [imath]\dfrac{AB}{EB} = \dfrac{AC}{FC}[/imath]
b) Định lý Talet đảo:
* Phát biểu: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
* Xét tam giác ABC có [imath]E\in AB ; F\in AC[/imath] và thỏa mãn 1 trong 3 tỉ lệ thức: [imath]\dfrac{AE}{AB} = \dfrac{AF}{AC}[/imath] , [imath]\dfrac{AE}{EB} = \dfrac{AF}{FC}[/imath], [imath]\dfrac{AB}{EB} = \dfrac{AC}{FC}[/imath].
Theo định lý Talet đảo, ta có : [imath]EF // BC[/imath]
c) Hệ quả định lý Talet
* Phát biểu: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.
* Xét tam giác ABC có: [imath]EF // BC (E\in AB; F\in AC)[/imath]
Theo hệ quả định lý Talet, ta có: [imath]\dfrac{AE}{AB} = \dfrac{AF}{AC} = \dfrac{EF}{BC}[/imath]
* Bài toán vẫn đúng với trường hợp đường thẳng cắt phần kéo dài của 2 cạnh tam giác, cụ thể như sau:
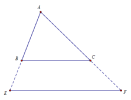
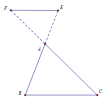
Với 2 trường hợp kể trên thì, với [imath]EF // BC[/imath], [imath]\dfrac{AE}{AB} = \dfrac{AF}{AC} = \dfrac{EF}{BC}[/imath] vẫn đúng.
3. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC
a) Định lý:Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
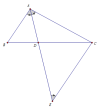
b) Chứng minh:
Kẻ [imath]CE // AB (E \in AD) \Rightarrow BAD = AEC[/imath] (2 góc so le trong)
Mà [imath]BAD = DAC \Rightarrow AEC = DAC \Rightarrow \Delta ACE[/imath] cân tại C
Hay [imath]CA = CE[/imath]
Xét [imath]\Delta ABD[/imath] có [imath]EC // AB[/imath], theeo hệ quả của định lý Talet
[imath]\Rightarrow \dfrac{BD}{DC} = \dfrac{AB}{EC} = \dfrac{AB}{AC}[/imath]
c) Chú ý
- Bài toán vẫn còn đúng với trường hợp phân giác ngoài, cụ thể:
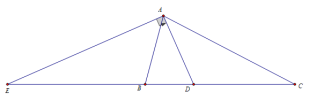
Xét [imath]\Delta ABC[/imath] có AD là phân giác ngoài, AE là phân giác trong.
Từ đó suy ra [imath]\dfrac{AB}{AC} = \dfrac{BD}{DC} = \dfrac{EB}{EC}[/imath]
- Từ đẳng thức trên còn suy ra tích [imath]BD.EC = DC.BE[/imath] , được sử dụng nhiều trong chứng minh đẳng thức hình học, nếu trong đó có sự xuất hiện của yếu tố phân giác, hoặc 2 đường vuông góc (nên nhớ phân giác trong và phân giác ngoài vuông góc với nhau)
4. TAM GIÁC ĐỒNG DẠNG
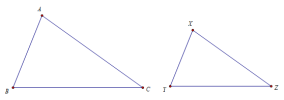
a) Định nghĩa 2 tam giác đồng dạng, chuyển thể:
* Định nghĩa 2 tam giác đồng dạng : Hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.
Cụ thể, xét [imath]\Delta ABC, \Delta XYZ[/imath] thỏa mãn [imath]\dfrac{AB}{XY} = \dfrac{BC}{YZ} = \dfrac{CA}{ZX}[/imath] và góc [imath]A = X; B=Y ; C=Z[/imath]
thì [imath]\Delta ABC \sim \Delta XYZ[/imath]
* Hệ quả định lý Talet, dưới ngôn ngữ tam giác đồng dạng:
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Ở đây mình không đề cập lại cụ thể ra sao nữa, các bạn có thể xem lại phần trước.
b) Trường hợp đồng dạng thứ nhất (cạnh - cạnh - cạnh)
* Phát biểu: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Cụ thể, xét [imath]\Delta ABC , \Delta XYZ[/imath] có: [imath]\dfrac{AB}{XY} = \dfrac{BC}{YZ} = \dfrac{CA}{ZX}[/imath] thì [imath]\Delta ABC \sim \Delta XYZ (c.c.c)[/imath]
c) Trường hợp đồng dạng thứ hai (cạnh - góc - cạnh)
* Phát biểu: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng theo trường hợp cạnh-góc-cạnh.
Cụ thể, xét [imath]\Delta ABC , \Delta XYZ[/imath] có: [imath]\dfrac{AB}{XY} = \dfrac{CA}{ZX}[/imath] và góc [imath]A =X[/imath] thì [imath]\Delta ABC \sim \Delta XYZ (c.g.c)[/imath]
d) Trường hợp đồng dạng thứ ba (góc - góc)
* Phát biểu: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đồng dạng.
Cụ thể, xét [imath]\Delta ABC , \Delta XYZ[/imath] có: góc [imath]A = X ; B = Y[/imath] thì [imath]\Delta ABC \sim \Delta XYZ (g.g)[/imath]
e) Trường hợp đồng dạng đặc biệt của tam giác vuông
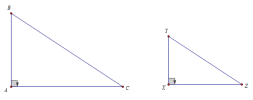
* Phát biểu: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đồng dạng.
Cụ thể, xét [imath]\Delta ABC , \Delta XYZ[/imath] vuông lần lượt tại A và X, có: [imath]\dfrac{AB}{BC} = \dfrac{XY}{YZ}[/imath]
[imath]\Rightarrow \Delta ABC \sim \Delta XYZ (ch-cgv)[/imath]
5. TÍNH CHẤT 2 TAM GIÁC ĐỒNG DẠNG
- Theo định nghĩa, hai tam giác đồng dạng sẽ có 3 cặp góc bằng nhau và 3 cặp cnahj tương ứng tỉ lệ.- Ngoài ra, các tỉ số đường tương ứng hạ từ các đỉnh tương ứng của 2 tam giác (như đường cao, đường trung tuyến, đường phân giác) bằng tỉ số đồng dạng.
Tỉ số diện tích 2 tam giác đồng dạng là bình phương tỉ số đồng dạng,
