[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Xin chào các bạn 
Ở bài viết này mình sẽ tổng hợp kiến thức cơ bản về chương III cho các bạn nhé.
I. Phương trình đường thẳng
- Vecto chỉ phương của đường thẳng d là vecto có giá trùng hoặc song song với đường thẳng d .
- Nhận xét:
+ Một đường thẳng có vô số vecto chỉ phương.
+ Một đường thẳng sẽ xác định nếu biết 1 điểm trên đường thẳng và 1 vecto chỉ phương của nó.
- Phương trình tham số của đường thẳng đi qua [imath]\overrightarrow{u}=(a,b)[/imath] và có vecto chỉ phương là [imath]\begin{cases} x=x_0+at \\ y=y_0+bt \end{cases}[/imath]
- Nếu đường thẳng d có vecto chỉ phương là thì tỉ số [imath]k=\dfrac{b}{a}[/imath] được gọi là hệ số góc của đường thẳng d.
- Phương trình đường thẳng có hệ số góc [imath]k[/imath] và đi qua điểm [imath]M(x_0,y_0)[/imath] là [imath]x-x_0=k(y-y_0)[/imath]
- Vecto pháp tuyến của đường thẳng là vecto có giá vuông góc với đường thẳng .
- Phương trình tổng quát của đường thẳng đi qua điểm [imath]M(x_0,y_0)[/imath] và có vecto pháp tuyến [imath]\overrightarrow{n}=(a,b)[/imath] là [imath]a(x-x_0)+b(y-y_0)=0[/imath]
- Đường thẳng đi qua [imath]A(a,0),B(0,b)[/imath] với [imath]a,b \neq 0[/imath] có phương trình là [imath]\dfrac{x}{a}+\dfrac{y}{b}=1[/imath].
(Phương trình đường thẳng này được gọi là phương trình đường thẳng theo đoạn chắn)
- Vị trí tương đối của 2 đường thẳng:
Cho [imath]{{\Delta }_{1}}:{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0,{{\Delta }_{2}}:{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0[/imath]. Số điểm chung của 2 đường thẳng là số nghiệm của hệ phương trình:
[math]\begin{cases} a_{1} x+b_1 y+c_1=0 \\ a_2 x+b_2 y+c_2=0 \end{cases}[/math]
- Khoảng cách từ điểm [imath]M(x_0,y_0)[/imath] đến đường thẳng [imath](d):ax+by+c=0[/imath] là [imath]{{d}_{(M,d)}}=\dfrac{|a{{x}_{0}}+b{{y}_{0}}+c|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}[/imath].
- Góc tạo bởi 2 đường thẳng [imath]\Delta_1, \Delta _2[/imath] có vecto pháp tuyến lần lượt là [imath]\overrightarrow{n_1}=(a_1,b_1), \overrightarrow{n_2}=(a_2,b_2)[/imath] được xác định bởi [imath]\cos \varphi =\dfrac{|\overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}}|}{|\overrightarrow{{{n}_{1}}}|.|\overrightarrow{{{n}_{2}}}|}=\dfrac{|{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}|}{\sqrt{a_{1}^{2}+b_{1}^{2}}.\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
- Phương trình đường thẳng phân giác của góc hợp bởi 2 đường thẳng:
Cho [imath]{{\Delta }_{1}}:{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0,{{\Delta }_{2}}:{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0[/imath]. Khi đó phương trình đường phân giác của góc tạo bởi [imath]\Delta_1, \Delta _2[/imath] có dạng [imath]\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
+ Nếu góc tạo bởi 2 đường thẳng là góc nhọn thì phương trình đường phân giác là [imath]\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
+ Nếu góc tạo bởi 2 đường thẳng là góc tù thì phương trình đường phân giác là [imath]\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=-\dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
II. Phương trình đường tròn
- Phương trình đường tròn tâm [imath]I(a,b)[/imath] và bán kính [imath]R[/imath] là [imath]{{(x-a)}^{2}}+{{(y-b)}^{2}}={{R}^{2}}[/imath].
- Nhận xét:
+ Phương trình đường tròn có thể viết lại thành [imath]{{x}^{2}}+{{y}^{2}}-2ax-2by+c=0[/imath] với [imath]c={{a}^{2}}+{{b}^{2}}-{{R}^{2}}[/imath]
+ Phương trình dạng [imath]{{x}^{2}}+{{y}^{2}}-2ax-2by+c=0[/imath] là phương trình đường tròn [imath]\Leftrightarrow c < a^2+b^2[/imath]
- Đường thẳng d là tiếp tuyến của đường tròn [imath](I,R)[/imath] [imath]\Leftrightarrow {{d}_{(I,d)}}=R[/imath]
- Phương trình tiếp tuyến của đường tròn [imath]{{(x-a)}^{2}}+{{(y-b)}^{2}}={{R}^{2}}[/imath] tại điểm [imath]M(x_0,y_0)[/imath] trên đường tròn là [imath]({{x}_{0}}-a)(x-{{x}_{0}})+({{y}_{0}}-b)(y-{{y}_{0}})=0[/imath].
III. Phương trình đường elip
- Định nghĩa: Cho 2 điểm [imath]{{F}_{1}},{{F}_{2}}\in Ox[/imath] đối xứng nhau qua trục [imath]Oy[/imath] . Khi đó quỹ tích điểm M thỏa mãn [imath]M{{F}_{1}}+M{{F}_{2}}=2a>2{{F}_{1}}{{F}_{2}}[/imath] là một đường elip.
- Cho [imath]{{F}_{1}}=(0,-c),{{F}_{2}}=(0,c)(c>0)[/imath] thì phương trình chính tắc đường elip quỹ tích điểm M là [imath]\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1[/imath] với [imath]a>b>0,{{a}^{2}}={{b}^{2}}+{{c}^{2}}[/imath].
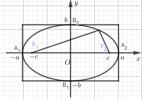
- Các thành phần của đường elip:
+ Điểm [imath]{{F}_{1}},{{F}_{2}}[/imath] được gọi là tiêu điểm của đường elip.
+ [imath]{{A}_{1}}(-a,0),{{A}_{2}}(a,0),{{B}_{1}}(0,-b),{{B}_{2}}(0,b)[/imath] được gọi là đỉnh của đường elip.
+ Độ dài của trục lớn là [imath]{{A}_{1}}{{A}_{2}}=2a[/imath], độ dài của trục nhỏ là [imath]{{B}_{1}}{{B}_{2}}=2b[/imath].
+ Tiêu cự của đường elip là [imath]{{F}_{1}}{{F}_{2}}=2c[/imath].
+ Tâm sai của đường elip là [imath]e=\dfrac{c}{a}[/imath].
+ Trục đối xứng của elip là [imath]Ox,Oy[/imath].
+ Tâm đối xứng của elip là [imath]O[/imath].
+ Hình chữ nhật bị giới hạn bởi [imath]x=\pm a,y=\pm b[/imath] được gọi là hình chữ nhật cơ sở của đường elip. Mọi điểm thuộc đường elip luôn nằm trong hình chữ nhật này.
Ở bài viết này mình sẽ tổng hợp kiến thức cơ bản về chương III cho các bạn nhé.I. Phương trình đường thẳng
- Vecto chỉ phương của đường thẳng d là vecto có giá trùng hoặc song song với đường thẳng d .
- Nhận xét:
+ Một đường thẳng có vô số vecto chỉ phương.
+ Một đường thẳng sẽ xác định nếu biết 1 điểm trên đường thẳng và 1 vecto chỉ phương của nó.
- Phương trình tham số của đường thẳng đi qua [imath]\overrightarrow{u}=(a,b)[/imath] và có vecto chỉ phương là [imath]\begin{cases} x=x_0+at \\ y=y_0+bt \end{cases}[/imath]
- Nếu đường thẳng d có vecto chỉ phương là thì tỉ số [imath]k=\dfrac{b}{a}[/imath] được gọi là hệ số góc của đường thẳng d.
- Phương trình đường thẳng có hệ số góc [imath]k[/imath] và đi qua điểm [imath]M(x_0,y_0)[/imath] là [imath]x-x_0=k(y-y_0)[/imath]
- Vecto pháp tuyến của đường thẳng là vecto có giá vuông góc với đường thẳng .
- Phương trình tổng quát của đường thẳng đi qua điểm [imath]M(x_0,y_0)[/imath] và có vecto pháp tuyến [imath]\overrightarrow{n}=(a,b)[/imath] là [imath]a(x-x_0)+b(y-y_0)=0[/imath]
- Đường thẳng đi qua [imath]A(a,0),B(0,b)[/imath] với [imath]a,b \neq 0[/imath] có phương trình là [imath]\dfrac{x}{a}+\dfrac{y}{b}=1[/imath].
(Phương trình đường thẳng này được gọi là phương trình đường thẳng theo đoạn chắn)
- Vị trí tương đối của 2 đường thẳng:
Cho [imath]{{\Delta }_{1}}:{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0,{{\Delta }_{2}}:{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0[/imath]. Số điểm chung của 2 đường thẳng là số nghiệm của hệ phương trình:
[math]\begin{cases} a_{1} x+b_1 y+c_1=0 \\ a_2 x+b_2 y+c_2=0 \end{cases}[/math]
- Khoảng cách từ điểm [imath]M(x_0,y_0)[/imath] đến đường thẳng [imath](d):ax+by+c=0[/imath] là [imath]{{d}_{(M,d)}}=\dfrac{|a{{x}_{0}}+b{{y}_{0}}+c|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}[/imath].
- Góc tạo bởi 2 đường thẳng [imath]\Delta_1, \Delta _2[/imath] có vecto pháp tuyến lần lượt là [imath]\overrightarrow{n_1}=(a_1,b_1), \overrightarrow{n_2}=(a_2,b_2)[/imath] được xác định bởi [imath]\cos \varphi =\dfrac{|\overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}}|}{|\overrightarrow{{{n}_{1}}}|.|\overrightarrow{{{n}_{2}}}|}=\dfrac{|{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}|}{\sqrt{a_{1}^{2}+b_{1}^{2}}.\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
- Phương trình đường thẳng phân giác của góc hợp bởi 2 đường thẳng:
Cho [imath]{{\Delta }_{1}}:{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0,{{\Delta }_{2}}:{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0[/imath]. Khi đó phương trình đường phân giác của góc tạo bởi [imath]\Delta_1, \Delta _2[/imath] có dạng [imath]\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\pm \dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
+ Nếu góc tạo bởi 2 đường thẳng là góc nhọn thì phương trình đường phân giác là [imath]\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=\dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
+ Nếu góc tạo bởi 2 đường thẳng là góc tù thì phương trình đường phân giác là [imath]\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{\sqrt{a_{1}^{2}+b_{1}^{2}}}=-\dfrac{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}{\sqrt{a_{2}^{2}+b_{2}^{2}}}[/imath].
II. Phương trình đường tròn
- Phương trình đường tròn tâm [imath]I(a,b)[/imath] và bán kính [imath]R[/imath] là [imath]{{(x-a)}^{2}}+{{(y-b)}^{2}}={{R}^{2}}[/imath].
- Nhận xét:
+ Phương trình đường tròn có thể viết lại thành [imath]{{x}^{2}}+{{y}^{2}}-2ax-2by+c=0[/imath] với [imath]c={{a}^{2}}+{{b}^{2}}-{{R}^{2}}[/imath]
+ Phương trình dạng [imath]{{x}^{2}}+{{y}^{2}}-2ax-2by+c=0[/imath] là phương trình đường tròn [imath]\Leftrightarrow c < a^2+b^2[/imath]
- Đường thẳng d là tiếp tuyến của đường tròn [imath](I,R)[/imath] [imath]\Leftrightarrow {{d}_{(I,d)}}=R[/imath]
- Phương trình tiếp tuyến của đường tròn [imath]{{(x-a)}^{2}}+{{(y-b)}^{2}}={{R}^{2}}[/imath] tại điểm [imath]M(x_0,y_0)[/imath] trên đường tròn là [imath]({{x}_{0}}-a)(x-{{x}_{0}})+({{y}_{0}}-b)(y-{{y}_{0}})=0[/imath].
III. Phương trình đường elip
- Định nghĩa: Cho 2 điểm [imath]{{F}_{1}},{{F}_{2}}\in Ox[/imath] đối xứng nhau qua trục [imath]Oy[/imath] . Khi đó quỹ tích điểm M thỏa mãn [imath]M{{F}_{1}}+M{{F}_{2}}=2a>2{{F}_{1}}{{F}_{2}}[/imath] là một đường elip.
- Cho [imath]{{F}_{1}}=(0,-c),{{F}_{2}}=(0,c)(c>0)[/imath] thì phương trình chính tắc đường elip quỹ tích điểm M là [imath]\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1[/imath] với [imath]a>b>0,{{a}^{2}}={{b}^{2}}+{{c}^{2}}[/imath].
- Các thành phần của đường elip:
+ Điểm [imath]{{F}_{1}},{{F}_{2}}[/imath] được gọi là tiêu điểm của đường elip.
+ [imath]{{A}_{1}}(-a,0),{{A}_{2}}(a,0),{{B}_{1}}(0,-b),{{B}_{2}}(0,b)[/imath] được gọi là đỉnh của đường elip.
+ Độ dài của trục lớn là [imath]{{A}_{1}}{{A}_{2}}=2a[/imath], độ dài của trục nhỏ là [imath]{{B}_{1}}{{B}_{2}}=2b[/imath].
+ Tiêu cự của đường elip là [imath]{{F}_{1}}{{F}_{2}}=2c[/imath].
+ Tâm sai của đường elip là [imath]e=\dfrac{c}{a}[/imath].
+ Trục đối xứng của elip là [imath]Ox,Oy[/imath].
+ Tâm đối xứng của elip là [imath]O[/imath].
+ Hình chữ nhật bị giới hạn bởi [imath]x=\pm a,y=\pm b[/imath] được gọi là hình chữ nhật cơ sở của đường elip. Mọi điểm thuộc đường elip luôn nằm trong hình chữ nhật này.
