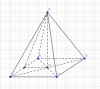
Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA= SB= SC =SD = [tex]\sqrt{2}[/tex]a. Tính góc giữa 2 mp (ABCD) và (SAB)
Hình chóp $S.ABCD$ có $SA= SB= SC =SD$
$\Rightarrow S.ABCD$ là hình chóp đều
$O=AC\cap BD\Rightarrow O$ là trung điểm của $AC,BD$
Suy ra $SO\bot (ABCD)$
$\Rightarrow SO\bot AO \Rightarrow SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt6}{2}$
$\Rightarrow AB\bot SO$
Gọi $E$ là trung điểm của $AB$
Suy ra $EO//AD$
$\Rightarrow OE\bot AB$
Suy ra $AB\bot (SEO)$
$\Rightarrow ((SAB);(ABCD))=\widehat{SEO}$
$\tan \widehat{SEO}=\dfrac{SO}{EO}=\sqrt6$
$\Rightarrow ((SAB);(ABCD))=\arctan \sqrt6$
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em có thể tham khảo thêm các kiến thức tại:
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
