Nhìn hình làm toán

[Thoòng Quốc An]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

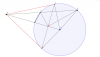
Nhìn hình vẽ, cm ba câu sau:
a) CM: Tứ giác OHEF nội tiếp
b) CM: HE.HF=HO.HM
c) CM: EI là phân giác góc HEM

HELP ME

 

[Thoòng Quốc An]

Đề: Qua điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA,MB ( A,B là các tiếp điểm) và cát tuyến MEF với (O) (E nằm giữa M và F và AE<BE) Gọi H là giao điểm OM và AB. Đoạn thẳng OM cắt (O) tại I
Cm ba câu trên!

 

[iceghost]

Gợi ý :
a) $MH \cdot MO = MA^2 = ME \cdot MF$, chứng minh một cặp tam giác đồng dạng nào đó, dùng dấu hiệu nhận biết tứ giác nội tiếp : góc ngoài bằng góc tại đỉnh đối trong
b) Có $\widehat{MHE} = \widehat{OFE}$, $\widehat{FHO} = \widehat{OEF}$, mà $\widehat{OFE} = \widehat{OEF}$ nên $\widehat{MHE} = \widehat{FHO}$
Kết hợp $\widehat{MEH} = \widehat{FOH}$ suy ra $\triangle{MEH} \sim \triangle{FOH}$ và suy ra đpcm
c) Ta có $\widehat{MEI} = \widehat{IBF}$, $\widehat{MEH} = \widehat{IOF}$, mà $\widehat{IOF} = 2\widehat{IBF}$ nên ta có đpcm