Toán Nhị thức Niu-tơn

[Chou Chou]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài 1: Tính tổng

[tex]A = 1.(C_{n}^{0})^{2} + 2.(C_{n}^{1})^{2} + ... + n.(C_{n}^{n})^{2}[/tex]
[tex]B = \frac{C_{n}^{0}}{1} + \frac{C_{n}^{1}}{2} + ... + \frac{C_{n}^{n}}{n+1}[/tex] (số hạng tổng quát)

Bài 2: Cho mạch điện như hình vẽ:


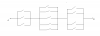
a) Có bao nhiêu cách để thông mạch từ A đến B
b) Có bao nhiêu cách để không thông mạch từ A đến B

Mọi người giúp em với ạ! Mai em học rồi! Cảm ơn trước ạ!
@cậu là của tớ??? @huuthuyenrop2 @thangnguyenst95 @lâm chấn phong @Trafalgar D Law

 

[cậu là của tớ???]

Bài 1: Tính tổng

[tex]A = 1.(C_{n}^{0})^{2} + 2.(C_{n}^{1})^{2} + ... + n.(C_{n}^{n})^{2}[/tex]
[tex]B = \frac{C_{n}^{0}}{1} + \frac{C_{n}^{1}}{2} + ... + \frac{C_{n}^{n}}{n+1}[/tex] (số hạng tổng quát)

Mọi người giúp em với ạ! Mai em học rồi! Cảm ơn trước ạ!
@cậu là của tớ??? @huuthuyenrop2 @thangnguyenst95

1.
2.thông cảm dù từng là.....nhưng tớ cx ko biết ct chữ C ở chỗ nào hjhj
1/(k+1)nCk=1/(n+1)*(n+1)C(k+1)
=>S=

 

[Chou Chou]

1.
2.thông cảm dù từng là.....nhưng tớ cx ko biết ct chữ C ở chỗ nào hjhj
1/(k+1)nCk=1/(n+1)*(n+1)C(k+1)
=>S=

Tui không hiểu gì cả, giải cụ thể đi @cậu là của tớ???

 

[cậu là của tớ???]

Tui không hiểu gì cả, giải cụ thể đi @cậu là của tớ???

đoạn đó xong rùi thế rô á
mà ko biết gõ chữ C ở đâu

 

[lengoctutb]

Bài 1: Tính tổng

[tex]A = 1.(C_{n}^{0})^{2} + 2.(C_{n}^{1})^{2} + ... + n.(C_{n}^{n})^{2}[/tex]
[tex]B = \frac{C_{n}^{0}}{1} + \frac{C_{n}^{1}}{2} + ... + \frac{C_{n}^{n}}{n+1}[/tex] (số hạng tổng quát)

Mọi người giúp em với ạ! Mai em học rồi! Cảm ơn trước ạ!
@cậu là của tớ??? @huuthuyenrop2 @thangnguyenst95

$b)$ Xét số hạng tổng quát $:$
$a_{k}=\frac{C_{n}^{k}}{k+1}=\frac{n!}{(k+1)k!.(n-k)!}=\frac{(n+1)n!}{(n+1)(k+1)k!.(n-k)!}=\frac{(n-1)!}{(n+1)(k+1)!.[(n+1)-(k+1)]!}=\frac{C_{n+1}^{k+1}}{n+1}$
Vậy $a_{k}=\frac{C_{n}^{k}}{k+1}=\frac{C_{n+1}^{k+1}}{n+1}$ $(1)$
Từ $(1)$$,$ ta có $:$ $\left\{\begin{matrix} \frac{C_{n}^{0}}{1}=\frac{C_{n+1}^{1}}{n+1}\\ \frac{C_{n}^{1}}{2}=\frac{C_{n+1}^{2}}{n+1}\\ \frac{C_{n}^{2}}{3}=\frac{C_{n+1}^{3}}{n+1}\\ \cdots \\ \frac{C_{n}^{n}}{n+1}=\frac{C_{n+1}^{n+1}}{n+1}\\ \end{matrix}\right.$
Vậy $B=\frac{C_{n+1}^{1}}{n+1}+\frac{C_{n+1}^{2}}{n+1}+\frac{C_{n+1}^{3}}{n+1}+\cdots +\frac{C_{n+1}^{n+1}}{n+1}=\frac{C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}}{n+1}$
$\Leftrightarrow (n+1).B=C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}$
$\Leftrightarrow (n+1).B+1=C_{n+1}^{0}+C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}$
$\Leftrightarrow (n+1).B+1=2^{n+1} \Leftrightarrow B=\frac{2^{n+1}-1}{n+1}$


Câu $a)$ bạn xem lại đề đi !

 

[Chou Chou]

$b)$ Xét số hạng tổng quát $:$
$a_{k}=\frac{C_{n}^{k}}{k+1}=\frac{n!}{(k+1)k!.(n-k)!}=\frac{(n+1)n!}{(n+1)(k+1)k!.(n-k)!}=\frac{(n-1)!}{(n+1)(k+1)!.[(n+1)-(k+1)]!}=\frac{C_{n+1}^{k+1}}{n+1}$
Vậy $a_{k}=\frac{C_{n}^{k}}{k+1}=\frac{C_{n+1}^{k+1}}{n+1}$ $(1)$
Từ $(1)$$,$ ta có $:$ $\left\{\begin{matrix} \frac{C_{n}^{0}}{1}=\frac{C_{n+1}^{1}}{n+1}\\ \frac{C_{n}^{1}}{2}=\frac{C_{n+1}^{2}}{n+1}\\ \frac{C_{n}^{2}}{3}=\frac{C_{n+1}^{3}}{n+1}\\ \cdots \\ \frac{C_{n}^{n}}{n+1}=\frac{C_{n+1}^{n+1}}{n+1}\\ \end{matrix}\right.$
Vậy $B=\frac{C_{n+1}^{1}}{n+1}+\frac{C_{n+1}^{2}}{n+1}+\frac{C_{n+1}^{3}}{n+1}+\cdots +\frac{C_{n+1}^{n+1}}{n+1}=\frac{C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}}{n+1}$
$\Leftrightarrow (n+1).B=C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}$
$\Leftrightarrow (n+1).B+1=C_{n+1}^{0}+C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}$
$\Leftrightarrow (n+1).B+1=2^{n+1} \Leftrightarrow B=\frac{2^{n+1}-1}{n+1}$


Câu $a)$ bạn xem lại đề đi !

câu 1 mình chép đúng đề rồi, không sai đâu @_@

 

[cậu là của tớ???]

Bài 2: Cho mạch điện như hình vẽ:

a) Có bao nhiêu cách để thông mạch từ A đến B
b) Có bao nhiêu cách để không thông mạch từ A đến B

thử lmf ahjhj
đy từ A=>B thì lần 1 là3 cc
lần 2là 5 cc
lần 3 là 4 cc
=>có 3.5.4=60 cc
b/là sao nhỉ
nhìn cái hình đó chả nhẽ mik đóng khóa K
hay là nhảy đường ko đy
khs hiểu quá đy
@thangnguyenst95 sao nhỉ
hay là đi qua cumj 1 nhưng ko qua cụm 2
và th2 đ qua cụm 1 ,2 nhưng ko qua cụm 3
th1 có 3 cc
th2 có 3.5=15
khó nghĩ ghê

$b)$ Xét số hạng tổng quát $:$
$a_{k}=\frac{C_{n}^{k}}{k+1}=\frac{n!}{(k+1)k!.(n-k)!}=\frac{(n+1)n!}{(n+1)(k+1)k!.(n-k)!}=\frac{(n-1)!}{(n+1)(k+1)!.[(n+1)-(k+1)]!}=\frac{C_{n+1}^{k+1}}{n+1}$
Vậy $a_{k}=\frac{C_{n}^{k}}{k+1}=\frac{C_{n+1}^{k+1}}{n+1}$ $(1)$
Từ $(1)$$,$ ta có $:$ $\left\{\begin{matrix} \frac{C_{n}^{0}}{1}=\frac{C_{n+1}^{1}}{n+1}\\ \frac{C_{n}^{1}}{2}=\frac{C_{n+1}^{2}}{n+1}\\ \frac{C_{n}^{2}}{3}=\frac{C_{n+1}^{3}}{n+1}\\ \cdots \\ \frac{C_{n}^{n}}{n}=\frac{C_{n+1}^{n+1}}{n+1}\\ \end{matrix}\right.$
Vậy $B=\frac{C_{n+1}^{1}}{n+1}+\frac{C_{n+1}^{2}}{n+1}+\frac{C_{n+1}^{3}}{n+1}+\cdots +\frac{C_{n+1}^{n+1}}{n+1}=\frac{C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}}{n+1}$
$\Leftrightarrow (n+1).B=C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}$
$\Leftrightarrow (n+1).B+1=C_{n+1}^{0}+C_{n+1}^{1}+C_{n+1}^{2}+C_{n+1}^{3}+\cdots +C_{n+1}^{n+1}
$\Leftrightarrow (n+1).B+1=2^{n+1} \Leftrightarrow B=\frac{2^{n+1}-1}{n+1}$


Câu $a)$ bạn xem lại đề đi !

 

[lengoctutb]

câu 1 mình chép đúng đề rồi, không sai đâu @_@

Mình nghĩ đề như thế này mới đúng chứ !
$A=1(C_{n}^{1})^{2}+2(C_{n}^{2})^{2}+3(C_{n}^{3})^{2}+\cdots+n(C_{n}^{n})^{2}$

 

[Chou Chou]

Mình nghĩ đề như thế này mới đúng chứ !
$A=1(C_{n}^{1})^{2}+2(C_{n}^{2})^{2}+3(C_{n}^{3})^{2}+\cdots+n(C_{n}^{n})^{2}$

có thể là mình chép sai đề trong vở rồi....
Bạn ơi, mình nghĩ là sửa ở chỗ $(n+1)(C_{n}^{n})^{2}$

 

[cậu là của tớ???]

Mình nghĩ đề như thế này mới đúng chứ !
$A=1(C_{n}^{1})^{2}+2(C_{n}^{2})^{2}+3(C_{n}^{3})^{2}+\cdots+n(C_{n}^{n})^{2}$

A=1.(C0n)2+2.(C1n)2+...+n.(Cnn)2

mình nghĩ đề đúng chỉ là mik cần t/g suy nghĩ

 

[fsdfsdf]

số hạng tổng quátk+1)C kn= n (C k-1 n-1) + C n k
thay vào là xong

 

[fsdfsdf]

câu dưới mạch không thông thì trong 1 đoạn mạch có 2 cái khóa hoặc hơn đóng í mà. tính số cách mắc được trừ đi 60 cách ở câu a là xong

 

[cậu là của tớ???]

S = 1(nC0)² + 2(nC1)² +... + n(nCn)² = (nCn)² +2 (nCn-1)² + ... + n(nC0)²
(do nCk = nCn-k với k = 0, 1, ..., n)

Áp dụng khai triển Newton có:
(1 + x)^n = nC0 + nC1 * x + nC2 * x^2 + ... + nCn * x^n
(1 + x)^n nhân (1 + x)^n=.....khai triển
mà (1+x)^2n=(1 + x)^n nhân (1 + x)^n=....khai triển
Suy ra hệ số của hạng tử chưá x^n n
ằm trong khia triển (1+x)^2n=>tổng ...khai tr=>tổng bài n(.....)
có lẽ vj

 

[Chou Chou]

câu dưới mạch không thông thì trong 1 đoạn mạch có 2 cái khóa hoặc hơn đóng í mà.

là sao?? giải thích rõ hơn đi bạn!

 

[fsdfsdf]

là sao?? giải thích rõ hơn đi bạn!

Có 2 cái khóa thì mạch bị đoản
P/S lâu lắm ms thấy bà

 

[Chou Chou]

Bài 2:
a) Mỗi khóa có 2 trạng thái đóng - mở nên:
(kí hiệu lần lượt (1), (2), (3) nhé)
- Khoang (1) có [tex]2^{3}-1[/tex] cách đóng - mở để khoang (1) có điện
- Khoang (2) có [tex]2^{5}-1[/tex] cách đóng - mở để khoang (2) có điện
- Khoang (3) có [tex]2^{4}-1[/tex] cách đóng - mở để khoang (3) có điện
Vậy có tất cả ([tex]2^{3}-1[/tex]) + ([tex]2^{5}-1[/tex]) + ([tex]2^{4}-1[/tex]) = 3255 cách để thông mạch
b) [tex]2^{12} - 3255[/tex] = 841 cách để không thông mạch

@tôi là ai? @fsdfsdf