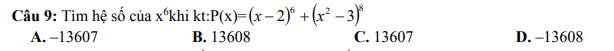Câu 9
[imath]P(x)=(x-2)^6+(x^2-3)^8 \\
\displaystyle = \sum^{6}_{k=0}{C^6_k x^k(-2)^{6-k}} + \sum^{8}_{l=0}{C^8_l (x^2)^l(-3)^{8-l}}[/imath]
[imath] \displaystyle = \sum^{6}_{k=0}{C^6_k (-1)^{6-k}.2^{6-k}x^k} + \sum^{8}_{l=0}{C^8_l(-1)^{8-l}.3^{8-l}x^{2l}}[/imath]
Hệ số của [imath]x^6[/imath] ứng với: [imath]k=6[/imath] và [imath] 2l=6 \Leftrightarrow l=3[/imath]
Vậy hệ số của [imath]x^6[/imath] trong khai triển của [imath]P(x)[/imath] là: [imath]C^6_6 (-1)^{6-6}.2^{6-6} + C^8_3(-1)^{8-3}.3^{8-3} = -13608[/imath]
Câu 2
Ta có: [imath](1-1)^{2n}=C^0_{2n}-C^1_{2n}+...-C^{2n-1}_{2n}+C^{2n}_{2n}[/imath],
[imath](1+1)^{2n}=C^0_{2n}+C^1_{2n}+...+C^{2n-1}_{2n}+C^{2n}_{2n}[/imath]
[imath]\Rightarrow C^1_{2n} + C^3_{2n}+ ...+ C^{2n-1}_{2n}=2^{2n-1}[/imath]
Lại có [imath]C^1_{2n} + C^3_{2n}+ ...+ C^{2n-1}_{2n}=8192 \\
\Leftrightarrow 2^{2n-1}=2^{13} \\
\Leftrightarrow n=7[/imath]
Do đó [imath]P(x)= \left ( 2x^3 - \dfrac{1}{x^4} \right )^7[/imath]
[imath]P(x)= \left ( 2x^3 - \dfrac{1}{x^4} \right )^7=(2x^3-x^{-4})^7 \\
\displaystyle = \sum^{7}_{k=0}{C^7_k (2x^3)^k (-x^{-4})^{7-k}}[/imath]
[imath]\displaystyle = \sum^{7}_{k=0}{C^7_k .2^k(x^3)^k .(-1)^{7-k}(x^{-4})^{7-k}}[/imath]
[imath]\displaystyle = \sum^{7}_{k=0}{C^7_k .2^k.(-1)^{7-k}. x^{3k}.x^{-28+4k}} \\
\displaystyle = \sum^{7}_{k=0}{C^7_k .2^k.(-1)^{7-k}. x^{7k-28}}[/imath]
Số hạng không chứa [imath]x[/imath] ứng với [imath]7k-28=0 \Leftrightarrow k=4[/imath]
Vậy số hạng không chứa [imath]x[/imath] trong khai triển của [imath]P(x)[/imath] là: [imath]C^7_4 .2^4(-1)^{7-4} = -560[/imath]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
