- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Đối với hàm bậc 3, hàm trùng phương, thì do đặc trưng dạng đồ thị dễ nhớ. Nên các bạn có thể áp dụng mẹo sau để giải quyết nhanh hơn 1 chút. Tiết kiệm thời gian để làm các câu khó .
* Hàm số bậc 3 dạng: [TEX]x^3+ax^2+bx+c[/TEX]
Do hệ số gắn với [TEX]x^3[/TEX] là dương nên khi có 2 cực trị, dạng đồ thị ai cũng biết nó là như thế này
Vậy rõ ràng là , điểm cực đại luôn luôn là điểm có hoành độ x nhỏ hơn trong 2 nghiệm. Vậy khi ta xác định được nghiệm f'(x)=0 , miễn cần trục xét dấu, ta biết được luôn đâu là cực đại, cực tiểu.
*Với hàm bậc 3 dạng : [TEX]-x^3+ax^2+bx+c[/TEX]
Hệ số gắn với [TEX]x^3[/TEX] âm nên khi đồ thị có 2 cực trị thì nó sẽ trông như thế này:
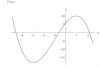
Do vậy, nên khi tìm ra 2 cực trị, thằng nào có hoành độ nhỏ hơn thì chắc chắn nó là cực tiểu, còn hoành độ lớn hơn sẽ là cực đại
Ví dụ : Tìm m để hàm số [TEX]-x^3+3mx^2-mx+6[/TEX] có 2 điểm CĐ, CT thỏa mãn [TEX]x_{cd}+3.x_{ct}=6[/TEX]
Lời giải:
f'(x)=[TEX]-3x^2+6mx-m[/TEX]
Sử dung delta tìm nghiệm, ta sẽ có được :
[tex]x_1= m+\frac{\sqrt{9m^2-3m}}{3};x_2=m-\frac{\sqrt{9m^2-3m}}{3}[/tex]
Vì hệ số của [TEX]x^3[/TEX] làm âm nên ta có x cực đại sẽ là nghiệm x lớn hơn trong 2 nghiệm. Vậy ta có:
[tex]x_{cd}=m+\frac{\sqrt{9m^2-3m}}{3}; x_{ct}=m-\frac{\sqrt{9m^2-3m}}{3}[/tex]
Vậy : [tex]x_{cd}+3x_{ct}=6<=>(m+\frac{\sqrt{9m^2-3m}}{3})+3(m-\frac{\sqrt{9m^2-3m}}{3})=6 <=>6m-9=\sqrt{9m^2-3m}[/tex]
Lúc này, đặt điều kiện [TEX]m \geq 1,5[/TEX] rồi bình phương 2 vế, là ta sẽ giải được có duy nhất 1 giá trị của m thỏa mãn
Lưu ý: Nếu bạn nào sử dụng Vi-ét để tìm m: [tex]x_1+3x_2=6[/tex] thì sẽ dẫn đến tìm thừa ra 1 giá trị của m. Bởi vì ta không biết chắc được [TEX]x_2[/TEX] nó là cực tiểu hay cực đại để thỏa mãn hệ thức yêu cầu. Do vậy ai làm theo Vi-ét thì khi làm xong vẫn cần bước thay m vào kiểm thử xem đúng là cực cực tiểu hay chưa.
Còn dạng hàm trùng phương, cái này còn dễ nhớ và nhận ra hơn cả hàm bậc 3.
*Hàm trùng phương dạng: [TEX]x^4+ax^2+b[/TEX] , hệ số gắn với [TEX]x^4[/TEX]>0 nên khi có 3 cực trị, dạng đồ thị nó sẽ như thế này:
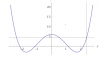
Vậy biết luôn 2 nghiệm x khác 0 của phương trình [TEX]f ' (x) =0 [/TEX] thì sẽ là 2 cực tiểu của đồ thị
*Với hàm trùng phương dạng : [TEX]-x^4+ax^2+b[/TEX]:
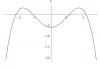
Vậy 2 nghiệm khác 0 của phương trình [TEX]f ' (x) =0 [/TEX] sẽ là 2 cực đại của đồ thị
* Hàm số bậc 3 dạng: [TEX]x^3+ax^2+bx+c[/TEX]
Do hệ số gắn với [TEX]x^3[/TEX] là dương nên khi có 2 cực trị, dạng đồ thị ai cũng biết nó là như thế này
Vậy rõ ràng là , điểm cực đại luôn luôn là điểm có hoành độ x nhỏ hơn trong 2 nghiệm. Vậy khi ta xác định được nghiệm f'(x)=0 , miễn cần trục xét dấu, ta biết được luôn đâu là cực đại, cực tiểu.
*Với hàm bậc 3 dạng : [TEX]-x^3+ax^2+bx+c[/TEX]
Hệ số gắn với [TEX]x^3[/TEX] âm nên khi đồ thị có 2 cực trị thì nó sẽ trông như thế này:
Do vậy, nên khi tìm ra 2 cực trị, thằng nào có hoành độ nhỏ hơn thì chắc chắn nó là cực tiểu, còn hoành độ lớn hơn sẽ là cực đại
Ví dụ : Tìm m để hàm số [TEX]-x^3+3mx^2-mx+6[/TEX] có 2 điểm CĐ, CT thỏa mãn [TEX]x_{cd}+3.x_{ct}=6[/TEX]
Lời giải:
f'(x)=[TEX]-3x^2+6mx-m[/TEX]
Sử dung delta tìm nghiệm, ta sẽ có được :
[tex]x_1= m+\frac{\sqrt{9m^2-3m}}{3};x_2=m-\frac{\sqrt{9m^2-3m}}{3}[/tex]
Vì hệ số của [TEX]x^3[/TEX] làm âm nên ta có x cực đại sẽ là nghiệm x lớn hơn trong 2 nghiệm. Vậy ta có:
[tex]x_{cd}=m+\frac{\sqrt{9m^2-3m}}{3}; x_{ct}=m-\frac{\sqrt{9m^2-3m}}{3}[/tex]
Vậy : [tex]x_{cd}+3x_{ct}=6<=>(m+\frac{\sqrt{9m^2-3m}}{3})+3(m-\frac{\sqrt{9m^2-3m}}{3})=6 <=>6m-9=\sqrt{9m^2-3m}[/tex]
Lúc này, đặt điều kiện [TEX]m \geq 1,5[/TEX] rồi bình phương 2 vế, là ta sẽ giải được có duy nhất 1 giá trị của m thỏa mãn
Lưu ý: Nếu bạn nào sử dụng Vi-ét để tìm m: [tex]x_1+3x_2=6[/tex] thì sẽ dẫn đến tìm thừa ra 1 giá trị của m. Bởi vì ta không biết chắc được [TEX]x_2[/TEX] nó là cực tiểu hay cực đại để thỏa mãn hệ thức yêu cầu. Do vậy ai làm theo Vi-ét thì khi làm xong vẫn cần bước thay m vào kiểm thử xem đúng là cực cực tiểu hay chưa.
Còn dạng hàm trùng phương, cái này còn dễ nhớ và nhận ra hơn cả hàm bậc 3.
*Hàm trùng phương dạng: [TEX]x^4+ax^2+b[/TEX] , hệ số gắn với [TEX]x^4[/TEX]>0 nên khi có 3 cực trị, dạng đồ thị nó sẽ như thế này:
Vậy biết luôn 2 nghiệm x khác 0 của phương trình [TEX]f ' (x) =0 [/TEX] thì sẽ là 2 cực tiểu của đồ thị
*Với hàm trùng phương dạng : [TEX]-x^4+ax^2+b[/TEX]:
Vậy 2 nghiệm khác 0 của phương trình [TEX]f ' (x) =0 [/TEX] sẽ là 2 cực đại của đồ thị
