Ý 1 là nguyên hàm từng phần 2 lần liên tiếp, đây là dạng khá kinh điển của từng phần, cụ thể có bạn đã làm rồi
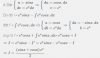
ý 2 thì ta dùng từng phần với
u=ln(x-1)=>[tex]u'=\frac{1}{x-1}[/tex]
dv=dx=> v= x-1
Từ đây giải dễ dàng rồi
ý 3 đặt ẩn : [tex]\sqrt{4+5lnx}=t=>2tdt=\frac{5}{x}dx[/tex] , đổi cận....
Mà [tex]\sqrt{4+5lnx}=t=>x=e^{\frac{t^2-4}{5}}=>2/5.t.e^{\frac{t^2-4}{5}}dt=dx[/tex]
thu được tích phân [tex]\int \frac{1}{5}t.e^{\frac{t^2-4}{5}}dt=\int \frac{1}{2}e^{\frac{t^2-4}{5}}d(\frac{t^2-4}{5})=\frac{1}{2}e^{\frac{t^2-4}{5}}[/tex]
Thay cận vào là ra
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.