- 22 Tháng tám 2021
- 1,199
- 2,904
- 346
- 22
- Gia Lai
- THPT Chuyên Hùng Vương
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Câu 1: Cho số phức z thoả mãn [imath]|z-1-i|+|z-3-2i| =\sqrt5[/imath]. Giá trị lớn nhất của [imath]|z+2i|[/imath] bằng...?
Lời giải:
Gọi [imath]z=x+yi[/imath] và điểm [imath]M(x,y)[/imath] là điểm biểu diễn z trên mặt phẳng toạ độ
Ta có: [imath]|z-1-i|+|z-3-2i|=\sqrt5[/imath]
[imath]\iff \sqrt{(x-1)^2+(y-1)^2} +\sqrt{(x-3)^2+(y-2)^2} = \sqrt5[/imath]
Đặt [imath]A(1;1), B(3;2)[/imath] thì từ (1) ta có: [imath]AM+BM=\sqrt5[/imath]
Mặt khác [imath]AB=\sqrt5[/imath]
Suy ra M thuộc đoạn thẳng AB
Lại có: [imath]|z+2i|=\sqrt{x^2+(y+2)^2} =MC[/imath] với [imath]C(0;-2)[/imath]
Suy ra [imath]|z+2i|_{\max}=CB=5[/imath]
Câu 2: Cho hai số phức [imath]z,w[/imath] thay đổi thoả mãn [imath]|z|=3, |z-w|=1[/imath]. Biết tập hợp điểm biểu diễn của số phức [imath]w[/imath] là hình phẳng H. Tính diện tích hình H.
Lời giải:
Gọi [imath]M,N[/imath] lần lượt là các điểm biểu diễn [imath]z[/imath] và [imath]w[/imath] trong mặt phẳng [imath]Oxy[/imath]
Từ giả thiết [imath]|z|=3, |z-w|=1[/imath] suy ra [imath]OM=3[/imath] và [imath]MN=1[/imath]
Ta có [imath]OM-MN \le ON \le OM+MN[/imath]
[imath]\implies 2 \le ON \le 4[/imath]
Do [imath]|w| = ON[/imath] suy ra N thuộc hình vành khăn
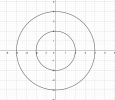
[imath]\implies H[/imath] là hình vành khăn giới hạn bởi hai đường tròn bán kính lần lượt là [imath]r=2,R=4[/imath]
[imath]S_H=\pi R^2-\pi r^2=\pi 4^2-\pi 2^2=12 \pi[/imath]
Câu 3: Gọi S là tập hợp các số thực m để phương trình [imath]z^2+3z+m^2-2m=0[/imath] có một nghiệm phức [imath]z_0[/imath] với [imath]|z_0|=2[/imath]. Tổng tất cả các phần tử trong S là
Lời giải:
TH1: [imath]z_0[/imath] là số thực
[imath]|z_0|=2 \iff \left[\begin{array}{l} z_0=2 \\ z_0=-2 \end{array}\right. \iff \left[\begin{array}{l} m^2-2m+10=0 (VN) \\ m^2-2m-2=0 \iff m=1 \pm \sqrt3 \end{array}\right.[/imath]
TH2: [imath]z_0[/imath] không phải là số thực
[imath]\iff \Delta=9-4(m^2-2m)<0 \iff m^2-2m>\dfrac{9}4[/imath] (1)
Vì phương trình [imath]z^2+3z+m^2-2m=0 \; (*)[/imath] có các hệ số thực và [imath]z_0[/imath] là nghiệm của [imath](*)[/imath] nên [imath]\overline{z_0}[/imath] cũng là nghiệm của [imath](*)[/imath]
Theo Vi-ét ta có [imath]z_0 .\overline{z_0}=m^2-2m \iff 4=|z_0|^2=m^2-2m[/imath] (thoả (1))
[imath]\iff m^2-2m-4=0 \iff m=1\pm \sqrt5[/imath]
Vậy tổng các phần tử của S bằng 4.
Câu 4: Cho số phức [imath]z[/imath] thoả mãn [imath]|4z+3i|=|4z-4+5i|[/imath]. Tìm giá trị nhỏ nhất của biểu thức [imath]P=|z+i|+|z-3i|[/imath]
Lời giải:
Đặt [imath]z=x+yi[/imath]. Từ giả thiết ta có [imath]|4z+3i|=|4z-4+5i|[/imath]
[imath]\iff |4x+4yi+3i| = |4x+4yi-4+5i| \iff |4x+(4y+3)i|=|4(x-1) +(4y+5)i|[/imath]
[imath]\iff 16x^2+(4y+3)^2=16(x-1)^2+(4y+5)^2 \iff 2x-y-2=0[/imath]
Suy ra tập hợp điểm biểu diễn các số phức z thoả mãn [imath]|4z+3i|=|4z-4+5i|[/imath] là đường thẳng [imath]\Delta : 2x-y-2=0[/imath]. Gọi [imath]M(x;y) \in \Delta, A(0;-1), B(0;3)[/imath] thì [imath]P=MA+MB[/imath]
Dễ thấy [imath]A,B[/imath] nằm cùng phía so với [imath]\Delta[/imath] nên nếu lấy điểm [imath]A'[/imath] đối xứng với [imath]A[/imath] qua [imath]\Delta[/imath] thì [imath]P[/imath] nhỏ nhất khi [imath]M[/imath] là giao điểm của [imath]A'B[/imath] và [imath]\Delta[/imath]. Khi đó [imath]\min P =A'B[/imath]
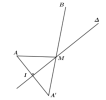
Phương trình [imath]AA': x+2y+2=0[/imath]
Toạ độ giao điểm [imath]I=\Delta \cap AA'[/imath] là nghiệm của hệ
[imath]\begin{cases} x+2y+2=0 \\ 2x-y-2=0 \end{cases} \iff \begin{cases} x=\dfrac{2}5 \\ y=-\dfrac{6}5\end{cases}[/imath]
[imath]\implies I\Big(\dfrac{2}5; -\dfrac{6}5\Big)[/imath]
[imath]\implies A' \Big(\dfrac{4}5; -\dfrac{7}5\Big)[/imath]
[imath]\implies \overrightarrow{A'B}=\Big(-\dfrac{4}5; \dfrac{22}5\Big)[/imath]
Vậy [imath]\min P=A'B=2\sqrt5[/imath]
Câu 5: Cho số phức [imath]z=a+bi \; (a;b \in \mathbb{R})[/imath] và thoả mãn [imath]|z-4-3i|=\sqrt5[/imath]. Tính [imath]P=a+b[/imath] khi [imath]|z+1-3i|+|z-1+i|[/imath] đạt giá trị lớn nhất.
Lời giải:
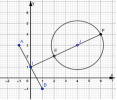
Gọi [imath]M(a,b)[/imath] là điểm biểu diễn số phức [imath]z=a+bi (a,b \in \mathbb{R})[/imath].
Có: [imath]|z-4-3i|=\sqrt5 \iff (a-4)^2 + (b-3)^2=5 \implies M \in (C): (x-4)^2+(y-3)^2=5[/imath]
Gọi [imath]A(-1;3)[/imath] là điểm biểu diễn số phức [imath]z_1=4+3i[/imath] và [imath]B(1;-1)[/imath] là điểm biểu diễn số phức [imath]z_2=1-i[/imath]. Gọi [imath]I(0;1)[/imath] là trung điểm đoạn AB .
[imath]\implies |z+1-3i|+|z-1+i|=MA+MB[/imath]
Có [imath](MA+MB)^2 \le (1+1)(MA^2+MB^2) \le 2 \Big(2MI^2+\dfrac{AB^2}{2} \Big)[/imath]
[imath]\implies |z+1-3i|+|z-1+i| \le \sqrt{4MI^2+AB^2}[/imath]
[imath]\implies |z+1-3i|+|z-1+i|[/imath] đạt GTLN khi [imath]MI[/imath] lớn nhất [imath]\iff M \equiv F[/imath].
Gọi [imath]J[/imath] là tâm đường tròn [imath](C), J(4;3), R=\sqrt5[/imath] .
Phương trình đường thẳng [imath]IJ: x-2y+2=0[/imath] . Tọa độ giao điểm của [imath](C)[/imath] và đường thẳng [imath]IJ[/imath] là nghiệm hệ pt: [imath]\begin{cases} x-2y+2=0 \\ (x-4)^2+(y-3)^2=5 \end{cases}[/imath]
[imath]\iff \begin{cases} x=2,y=2 \\ x=6, y=4 \end{cases}[/imath]
Gọi [imath]E(2;2), F(6;4)[/imath] có [imath]IE>IF[/imath]
Vậy [imath]M \equiv F(6;4) \implies z=6+4i \implies P=10[/imath]
________
Xem thêm Một số dạng vận dụng, vận dụng cao về cực trị của hàm số
Lời giải:
Gọi [imath]z=x+yi[/imath] và điểm [imath]M(x,y)[/imath] là điểm biểu diễn z trên mặt phẳng toạ độ
Ta có: [imath]|z-1-i|+|z-3-2i|=\sqrt5[/imath]
[imath]\iff \sqrt{(x-1)^2+(y-1)^2} +\sqrt{(x-3)^2+(y-2)^2} = \sqrt5[/imath]
Đặt [imath]A(1;1), B(3;2)[/imath] thì từ (1) ta có: [imath]AM+BM=\sqrt5[/imath]
Mặt khác [imath]AB=\sqrt5[/imath]
Suy ra M thuộc đoạn thẳng AB
Lại có: [imath]|z+2i|=\sqrt{x^2+(y+2)^2} =MC[/imath] với [imath]C(0;-2)[/imath]
Suy ra [imath]|z+2i|_{\max}=CB=5[/imath]
Câu 2: Cho hai số phức [imath]z,w[/imath] thay đổi thoả mãn [imath]|z|=3, |z-w|=1[/imath]. Biết tập hợp điểm biểu diễn của số phức [imath]w[/imath] là hình phẳng H. Tính diện tích hình H.
Lời giải:
Gọi [imath]M,N[/imath] lần lượt là các điểm biểu diễn [imath]z[/imath] và [imath]w[/imath] trong mặt phẳng [imath]Oxy[/imath]
Từ giả thiết [imath]|z|=3, |z-w|=1[/imath] suy ra [imath]OM=3[/imath] và [imath]MN=1[/imath]
Ta có [imath]OM-MN \le ON \le OM+MN[/imath]
[imath]\implies 2 \le ON \le 4[/imath]
Do [imath]|w| = ON[/imath] suy ra N thuộc hình vành khăn

[imath]\implies H[/imath] là hình vành khăn giới hạn bởi hai đường tròn bán kính lần lượt là [imath]r=2,R=4[/imath]
[imath]S_H=\pi R^2-\pi r^2=\pi 4^2-\pi 2^2=12 \pi[/imath]
Câu 3: Gọi S là tập hợp các số thực m để phương trình [imath]z^2+3z+m^2-2m=0[/imath] có một nghiệm phức [imath]z_0[/imath] với [imath]|z_0|=2[/imath]. Tổng tất cả các phần tử trong S là
Lời giải:
TH1: [imath]z_0[/imath] là số thực
[imath]|z_0|=2 \iff \left[\begin{array}{l} z_0=2 \\ z_0=-2 \end{array}\right. \iff \left[\begin{array}{l} m^2-2m+10=0 (VN) \\ m^2-2m-2=0 \iff m=1 \pm \sqrt3 \end{array}\right.[/imath]
TH2: [imath]z_0[/imath] không phải là số thực
[imath]\iff \Delta=9-4(m^2-2m)<0 \iff m^2-2m>\dfrac{9}4[/imath] (1)
Vì phương trình [imath]z^2+3z+m^2-2m=0 \; (*)[/imath] có các hệ số thực và [imath]z_0[/imath] là nghiệm của [imath](*)[/imath] nên [imath]\overline{z_0}[/imath] cũng là nghiệm của [imath](*)[/imath]
Theo Vi-ét ta có [imath]z_0 .\overline{z_0}=m^2-2m \iff 4=|z_0|^2=m^2-2m[/imath] (thoả (1))
[imath]\iff m^2-2m-4=0 \iff m=1\pm \sqrt5[/imath]
Vậy tổng các phần tử của S bằng 4.
Câu 4: Cho số phức [imath]z[/imath] thoả mãn [imath]|4z+3i|=|4z-4+5i|[/imath]. Tìm giá trị nhỏ nhất của biểu thức [imath]P=|z+i|+|z-3i|[/imath]
Lời giải:
Đặt [imath]z=x+yi[/imath]. Từ giả thiết ta có [imath]|4z+3i|=|4z-4+5i|[/imath]
[imath]\iff |4x+4yi+3i| = |4x+4yi-4+5i| \iff |4x+(4y+3)i|=|4(x-1) +(4y+5)i|[/imath]
[imath]\iff 16x^2+(4y+3)^2=16(x-1)^2+(4y+5)^2 \iff 2x-y-2=0[/imath]
Suy ra tập hợp điểm biểu diễn các số phức z thoả mãn [imath]|4z+3i|=|4z-4+5i|[/imath] là đường thẳng [imath]\Delta : 2x-y-2=0[/imath]. Gọi [imath]M(x;y) \in \Delta, A(0;-1), B(0;3)[/imath] thì [imath]P=MA+MB[/imath]
Dễ thấy [imath]A,B[/imath] nằm cùng phía so với [imath]\Delta[/imath] nên nếu lấy điểm [imath]A'[/imath] đối xứng với [imath]A[/imath] qua [imath]\Delta[/imath] thì [imath]P[/imath] nhỏ nhất khi [imath]M[/imath] là giao điểm của [imath]A'B[/imath] và [imath]\Delta[/imath]. Khi đó [imath]\min P =A'B[/imath]

Phương trình [imath]AA': x+2y+2=0[/imath]
Toạ độ giao điểm [imath]I=\Delta \cap AA'[/imath] là nghiệm của hệ
[imath]\begin{cases} x+2y+2=0 \\ 2x-y-2=0 \end{cases} \iff \begin{cases} x=\dfrac{2}5 \\ y=-\dfrac{6}5\end{cases}[/imath]
[imath]\implies I\Big(\dfrac{2}5; -\dfrac{6}5\Big)[/imath]
[imath]\implies A' \Big(\dfrac{4}5; -\dfrac{7}5\Big)[/imath]
[imath]\implies \overrightarrow{A'B}=\Big(-\dfrac{4}5; \dfrac{22}5\Big)[/imath]
Vậy [imath]\min P=A'B=2\sqrt5[/imath]
Câu 5: Cho số phức [imath]z=a+bi \; (a;b \in \mathbb{R})[/imath] và thoả mãn [imath]|z-4-3i|=\sqrt5[/imath]. Tính [imath]P=a+b[/imath] khi [imath]|z+1-3i|+|z-1+i|[/imath] đạt giá trị lớn nhất.
Lời giải:

Gọi [imath]M(a,b)[/imath] là điểm biểu diễn số phức [imath]z=a+bi (a,b \in \mathbb{R})[/imath].
Có: [imath]|z-4-3i|=\sqrt5 \iff (a-4)^2 + (b-3)^2=5 \implies M \in (C): (x-4)^2+(y-3)^2=5[/imath]
Gọi [imath]A(-1;3)[/imath] là điểm biểu diễn số phức [imath]z_1=4+3i[/imath] và [imath]B(1;-1)[/imath] là điểm biểu diễn số phức [imath]z_2=1-i[/imath]. Gọi [imath]I(0;1)[/imath] là trung điểm đoạn AB .
[imath]\implies |z+1-3i|+|z-1+i|=MA+MB[/imath]
Có [imath](MA+MB)^2 \le (1+1)(MA^2+MB^2) \le 2 \Big(2MI^2+\dfrac{AB^2}{2} \Big)[/imath]
[imath]\implies |z+1-3i|+|z-1+i| \le \sqrt{4MI^2+AB^2}[/imath]
[imath]\implies |z+1-3i|+|z-1+i|[/imath] đạt GTLN khi [imath]MI[/imath] lớn nhất [imath]\iff M \equiv F[/imath].
Gọi [imath]J[/imath] là tâm đường tròn [imath](C), J(4;3), R=\sqrt5[/imath] .
Phương trình đường thẳng [imath]IJ: x-2y+2=0[/imath] . Tọa độ giao điểm của [imath](C)[/imath] và đường thẳng [imath]IJ[/imath] là nghiệm hệ pt: [imath]\begin{cases} x-2y+2=0 \\ (x-4)^2+(y-3)^2=5 \end{cases}[/imath]
[imath]\iff \begin{cases} x=2,y=2 \\ x=6, y=4 \end{cases}[/imath]
Gọi [imath]E(2;2), F(6;4)[/imath] có [imath]IE>IF[/imath]
Vậy [imath]M \equiv F(6;4) \implies z=6+4i \implies P=10[/imath]
________
Xem thêm Một số dạng vận dụng, vận dụng cao về cực trị của hàm số

