- 10 Tháng mười một 2013
- 1,559
- 2,715
- 386
- 26
- Cần Thơ
- Đại học Cần Thơ
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Xin chào các bạn!
Dạo gần đây mình thấy một số chủ đề số phức ở một số bài đăng, có những bài khá phức tạp và nhiều khi cũng cảm thấy bó tay, không có cách biến đổi và cũng chẳng biết ý đồ người cho đề là gì...


Nhưng dù sao thì đây cũng là một vài kinh nghiệm của mình trong việc giải quyết những bài toán về số phức ở một số dạng, có thể các bạn đã biết rồi nhưng hãy xem qua và đóng góp một số bài toán cũng như các ý tưởng giải quyết của mình nhé, cảm ơn các bạn
Lưu ý: Bài viết này chỉ đưa lên bài toán cơ bản và cách giải quyết của mình, và của cá nhân mình thấy hợp lý (và có tham khảo từ sách vở và các nguồn thông tin khác). Mình xin phép không tổng quát hóa bài toán mà chính những người đọc sẽ tự tổng quát hóa cho bản thân mình nhé:
Sau đây là nội dung:
Bài 1: Số phức z thỏa |z - 3 - 4i| = 2 (*), tìm giá trị lớn nhất và giá trị nhỏ nhất của |z|
**1: Giải quyết theo cách truyền thống: Đặt z = a + bi
(*) => [tex] (a-3)^2 + (b-4)^2 = 4[/tex] (ai cũng biết, hihi)
Tới đây mình lại có 2 hướng giải quyết:
Cách thứ 1: Sử dụng bất đẳng thức Bunyakovsky:
Biến đổi: [tex](a-3)^2 + (b-4)^2 = 4 \Leftrightarrow a^2 + b^2 - 6a - 8b + 21 = 0 \Leftrightarrow a^2 + b^2 = 6a + 8b - 21[/tex], ta có
[tex](6(a-3) + 8(b-4))^2 \leq ((a-3)^2 + (b-4)^2) (6^2 + 8^2) = 4(6^2+8^2) \Leftrightarrow (6a+8b-50)^2 \leq 4.100 \Leftrightarrow -20 \leq 6a+8b-50 \leq 20 \Leftrightarrow 9 \leq 6a+8b-21 \leq 49 \Leftrightarrow 9 \leq |z|^2 \leq 49[/tex]
Từ đó => 3 <= |z| <= 7, điều kiện dấu "=" xảy ra <=> [tex]\frac{a-3}{6} = \frac{b-4}{8}[/tex], các bạn thế a, b vào tìm z giúp mình, nhưng đề bài không yêu cầu nên thôi.
Cách thứ 2: Đặt [tex]\left\{\begin{matrix} a = 3+2cos \theta\\ b = 4+2sin \theta \end{matrix}\right.[/tex], khi đó [tex]|z|^2 = a^2 + b^2[/tex] trở thành [tex]|z|^2 = (3 + 2 cos\theta)^2 + (4 + 2sin\theta)^2 = 29+2(6cos \theta + 8sin \theta)[/tex], tới đây các bạn có thể áp dụng Bunyakovsky vào để tìm giá trị lớn nhất và nhỏ nhất của lượng [tex] (6cos \theta + 8sin \theta) [/tex], hay ([tex](6cos \theta + 8sin \theta)^2 \leq (sin^2\theta + cos^2\theta) (6^2 + 8^2) = 100 \Leftrightarrow -10 \leq 6cos \theta + 8sin \theta \leq 10[/tex], hoặc có thể làm như thế này: [tex]6cos \theta + 8sin \theta = 10 (\frac{6}{10} cos\theta + \frac{8}{10} sin \theta) = 10 sin (arcsin \frac{6}{10} + \theta)[/tex] mà [tex]-1 \leq sin (arcsin \frac{6}{10} + \theta) \leq 1[/tex], nên suy ra [tex] -10 \leq 6cos \theta + 8sin \theta \leq 10 [/tex]. (Tại sao mình không rút gọn 6:8 thành 3:4 cho gọn, có lý do cả)
Cách thứ 3: Dùng hình học:
Hình phác họa: (Mình không dùng geo2d, vẽ paint cho tiện, các bạn thông cảm)

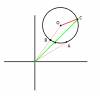
Dễ thấy quỹ tích z là một đường tròn tâm (I) bán kính R = 2, nhưng điều quan trọng là |z| là khoảng cách từ z đến gốc tọa độ. Dựng đoạn OI cắt (I) tại B, với (I) cố định, dĩ nhiên B cố định
Xét các tam giác OIA và OIC, ta dễ thấy [tex]OA + IA \geq IO \Leftrightarrow R + OA \geq R + OB \Leftrightarrow OA \geq OB[/tex]
[tex]OC \leq IO + IC = OB+2R[/tex]
Như vậy, dễ thấy: [tex]OB \leq |z| \leq OB + 2R[/tex]
Công việc tìm đoạn OB xin nhường lại cho bạn đọc!!!
2. Bài toán 2: Với z thỏa |z - 2 + 3i| = 2 thì tập z là một đường tròn, cho [tex]w = (1+i)z + 2 - i [/tex] thì tập các điểm biểu diễn w cũng là 1 đường tròn, tính bán kính đường tròn này.
Với cách truyền thống thì các bạn có thể biểu diễn z = a + bi rồi biến đổi w, mình chỉ biết chúc các bạn may mắn khi biến đổi (hoặc là mình chưa biết cách biến đổi sao cho nhanh và đỡ sai), nhưng trong bài này mình sẽ làm thế này:
[tex] w = (1+i)z + 2 - i \Leftrightarrow |w - 2 + i| = |(1+i)z| = |1+i||z| = 2\sqrt{2}[/tex]
Như vậy, dễ thấy tập điểm biểu diễn w là một đường tròn tâm P(2;-1) và bán kính là [tex] 2\sqrt{2}[/tex]
Nhận xét: việc phép đổi w từ z giống như 1 phép biến hình trong đó có tịnh tiến z và vị tự nó.
3. Bài toán 3: Cho z thỏa |z - 3 - 4i| = [tex]\sqrt{5}[/tex], tìm max và min của P = [tex]|z+2|^2 - |z-i|^2[/tex]
Mình vô tình thấy bài này trên internet, các bạn search có thể tìm ra, riêng cách giải quyết bài này người ta cũng đã có giải tất cả (với cách đặt P là giá trị tối ưu cần tìm), nhưng trong bài này mình đề nghị cách làm sau:
Sau khi biến đổi biết tập z là một đường tròn tâm I(3,4), bán kính căn 5, ta có thể đặt [tex]\left\{\begin{matrix} x = 3 + \sqrt{5}cos \theta\\ y = 4 + \sqrt{5}sin \theta \end{matrix}\right.[/tex], rồi sau đó tự động thế vào P sẽ được 1 biểu thức đơn giản theo [tex] cos \theta [/tex] và làm tiếp. Các bạn có thể trao đổi về bài này bên dưới nếu có trục trặc
Trên đây là 3 vấn đề nhỏ mà mình muốn trao đổi với các bạn, nếu có dịp mình sẽ đăng thêm các bài về giá trị lớn/nhỏ nhất của biểu thức số phức để chúng ta có thêm vũ khí để chống lại những vấn đề đó.
Mọi ý kiến đóng góp mình xin lắng nghe.
Chúc các bạn một buổi chiều vui vẻ:
Thân.
Dạo gần đây mình thấy một số chủ đề số phức ở một số bài đăng, có những bài khá phức tạp và nhiều khi cũng cảm thấy bó tay, không có cách biến đổi và cũng chẳng biết ý đồ người cho đề là gì...
Nhưng dù sao thì đây cũng là một vài kinh nghiệm của mình trong việc giải quyết những bài toán về số phức ở một số dạng, có thể các bạn đã biết rồi nhưng hãy xem qua và đóng góp một số bài toán cũng như các ý tưởng giải quyết của mình nhé, cảm ơn các bạn
Lưu ý: Bài viết này chỉ đưa lên bài toán cơ bản và cách giải quyết của mình, và của cá nhân mình thấy hợp lý (và có tham khảo từ sách vở và các nguồn thông tin khác). Mình xin phép không tổng quát hóa bài toán mà chính những người đọc sẽ tự tổng quát hóa cho bản thân mình nhé:
Sau đây là nội dung:
Bài 1: Số phức z thỏa |z - 3 - 4i| = 2 (*), tìm giá trị lớn nhất và giá trị nhỏ nhất của |z|
**1: Giải quyết theo cách truyền thống: Đặt z = a + bi
(*) => [tex] (a-3)^2 + (b-4)^2 = 4[/tex] (ai cũng biết, hihi)
Tới đây mình lại có 2 hướng giải quyết:
Cách thứ 1: Sử dụng bất đẳng thức Bunyakovsky:
Biến đổi: [tex](a-3)^2 + (b-4)^2 = 4 \Leftrightarrow a^2 + b^2 - 6a - 8b + 21 = 0 \Leftrightarrow a^2 + b^2 = 6a + 8b - 21[/tex], ta có
[tex](6(a-3) + 8(b-4))^2 \leq ((a-3)^2 + (b-4)^2) (6^2 + 8^2) = 4(6^2+8^2) \Leftrightarrow (6a+8b-50)^2 \leq 4.100 \Leftrightarrow -20 \leq 6a+8b-50 \leq 20 \Leftrightarrow 9 \leq 6a+8b-21 \leq 49 \Leftrightarrow 9 \leq |z|^2 \leq 49[/tex]
Từ đó => 3 <= |z| <= 7, điều kiện dấu "=" xảy ra <=> [tex]\frac{a-3}{6} = \frac{b-4}{8}[/tex], các bạn thế a, b vào tìm z giúp mình, nhưng đề bài không yêu cầu nên thôi.
Cách thứ 2: Đặt [tex]\left\{\begin{matrix} a = 3+2cos \theta\\ b = 4+2sin \theta \end{matrix}\right.[/tex], khi đó [tex]|z|^2 = a^2 + b^2[/tex] trở thành [tex]|z|^2 = (3 + 2 cos\theta)^2 + (4 + 2sin\theta)^2 = 29+2(6cos \theta + 8sin \theta)[/tex], tới đây các bạn có thể áp dụng Bunyakovsky vào để tìm giá trị lớn nhất và nhỏ nhất của lượng [tex] (6cos \theta + 8sin \theta) [/tex], hay ([tex](6cos \theta + 8sin \theta)^2 \leq (sin^2\theta + cos^2\theta) (6^2 + 8^2) = 100 \Leftrightarrow -10 \leq 6cos \theta + 8sin \theta \leq 10[/tex], hoặc có thể làm như thế này: [tex]6cos \theta + 8sin \theta = 10 (\frac{6}{10} cos\theta + \frac{8}{10} sin \theta) = 10 sin (arcsin \frac{6}{10} + \theta)[/tex] mà [tex]-1 \leq sin (arcsin \frac{6}{10} + \theta) \leq 1[/tex], nên suy ra [tex] -10 \leq 6cos \theta + 8sin \theta \leq 10 [/tex]. (Tại sao mình không rút gọn 6:8 thành 3:4 cho gọn, có lý do cả)
Cách thứ 3: Dùng hình học:
Hình phác họa: (Mình không dùng geo2d, vẽ paint cho tiện, các bạn thông cảm)

Dễ thấy quỹ tích z là một đường tròn tâm (I) bán kính R = 2, nhưng điều quan trọng là |z| là khoảng cách từ z đến gốc tọa độ. Dựng đoạn OI cắt (I) tại B, với (I) cố định, dĩ nhiên B cố định
Xét các tam giác OIA và OIC, ta dễ thấy [tex]OA + IA \geq IO \Leftrightarrow R + OA \geq R + OB \Leftrightarrow OA \geq OB[/tex]
[tex]OC \leq IO + IC = OB+2R[/tex]
Như vậy, dễ thấy: [tex]OB \leq |z| \leq OB + 2R[/tex]
Công việc tìm đoạn OB xin nhường lại cho bạn đọc!!!
2. Bài toán 2: Với z thỏa |z - 2 + 3i| = 2 thì tập z là một đường tròn, cho [tex]w = (1+i)z + 2 - i [/tex] thì tập các điểm biểu diễn w cũng là 1 đường tròn, tính bán kính đường tròn này.
Với cách truyền thống thì các bạn có thể biểu diễn z = a + bi rồi biến đổi w, mình chỉ biết chúc các bạn may mắn khi biến đổi (hoặc là mình chưa biết cách biến đổi sao cho nhanh và đỡ sai), nhưng trong bài này mình sẽ làm thế này:
[tex] w = (1+i)z + 2 - i \Leftrightarrow |w - 2 + i| = |(1+i)z| = |1+i||z| = 2\sqrt{2}[/tex]
Như vậy, dễ thấy tập điểm biểu diễn w là một đường tròn tâm P(2;-1) và bán kính là [tex] 2\sqrt{2}[/tex]
Nhận xét: việc phép đổi w từ z giống như 1 phép biến hình trong đó có tịnh tiến z và vị tự nó.
3. Bài toán 3: Cho z thỏa |z - 3 - 4i| = [tex]\sqrt{5}[/tex], tìm max và min của P = [tex]|z+2|^2 - |z-i|^2[/tex]
Mình vô tình thấy bài này trên internet, các bạn search có thể tìm ra, riêng cách giải quyết bài này người ta cũng đã có giải tất cả (với cách đặt P là giá trị tối ưu cần tìm), nhưng trong bài này mình đề nghị cách làm sau:
Sau khi biến đổi biết tập z là một đường tròn tâm I(3,4), bán kính căn 5, ta có thể đặt [tex]\left\{\begin{matrix} x = 3 + \sqrt{5}cos \theta\\ y = 4 + \sqrt{5}sin \theta \end{matrix}\right.[/tex], rồi sau đó tự động thế vào P sẽ được 1 biểu thức đơn giản theo [tex] cos \theta [/tex] và làm tiếp. Các bạn có thể trao đổi về bài này bên dưới nếu có trục trặc
Trên đây là 3 vấn đề nhỏ mà mình muốn trao đổi với các bạn, nếu có dịp mình sẽ đăng thêm các bài về giá trị lớn/nhỏ nhất của biểu thức số phức để chúng ta có thêm vũ khí để chống lại những vấn đề đó.
Mọi ý kiến đóng góp mình xin lắng nghe.
Chúc các bạn một buổi chiều vui vẻ:
Thân.