B
bigbang195
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài toán B.Đ.T thường là nội dung khó với các bạn học sinh trung học cơ sở .Một lí do
đơn giản vì đây là dạng toán ''mới mẻ'' với các bạn và khi giải các bài toán B.Đ.T các
bạn thường cảm thấy ''lúng túng'' không biết phải sử dụng phương pháp gì?Tuy nhiên,
trong nhiều bài toán B.Đ.t có điều kiện chúng ta có thể dựa vào điều kiện của biến để
đặt ẩn phụ đưa bài toán về dạng đơn giản có thể đánh giá được trực tiếp mà không cần
sử dụng đến các công cụ ''đao to búa lớn''. Bài viết dưới đây dựa trên ý tưởng của
My Teacher-thầy Hoàng văn Đắc
Chúng ta bắt đầu với một bài toán đơn giản sau
Ví dụ 1 .CMR Với
và
thì
Nhận xét rằng một biểu thức nhiều biến thường đạt giá trị lớn nhất hay nhỏ nhất khi tất
cả các biến bằng nhau ( tổng quát hơn là trường hợp một số biến bằng nhau) hoặc một
số biến có giá trị trên biên .Điều này gợi ý cho ta cách đổi biến như sau
Lời giải Do
nên có thể đặt
với
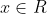
Ta có
^{4}+(2-x)^{4}=2x^{4}+48x^{2}+32 \geq 32)
(đpcm)
Đẳng thức xảy ra
.Như vậy bằng cách đổi biến thích hợp chúng ta đã
đưa bài toán về dạng đơn giản có thể đánh giá trực tiếp được và B.Đ.T chúng ta sử dụng chỉ là
B.Đ.T cơ bản nhất
Chúng ta sẽ gặp lại nhau sau ít phút quảng cáo
....
Trở lại với bài viết .Tiếp theo chúng ta xem xét một vài ví dụ khác.Qua đó hi vọng
các bạn học sinh THCS sẽ có được một cách nhìn mới với những bài toán B.Đ.T kiểu này.
Ví dụ 2.Cho
thỏa mãn
.CMR
Lời giải. Đặt
.Từ
ta có
B.Đ.T cần chứng minh tương đương với
^{3}+(1+y)^{3} \leq (1+x)^{4}+(1+y)^{4})
^{3}+y(1+y)^{3} \geq0)
(x^{2}-xy+y^{2})+3(x^{2}+y^{2})+x+y \geq 0)
(B.Đ.T này
đúng vì
)
Đẳng thức xảy ra
.
Ví dụ 3.Cho
thỏa mãn
.
CMR
Lời giải.Vì
nên có thể đặt
với
Ta có
^{2}+(1+y)^{2}+(1-x-y)^{2}+)
(1-y)+(1-y)(1-x-y)+(1-x-y)(1-x))
^{2}+\frac{3y^{2}}{4}+6\geq 6)
(đpcm)
Đẳng thức xảy ra
Ví dụ 4.Cho
thỏa mãn
.CMR
(b+d)+2ac+2bd \leq \frac{1}{2})
Lời giải.Vì
nên có thể đặt
Ta có
(b+d)+2ac+2bd)
(\frac{1}{2}-x-y)+2(\frac{1}{4}+x+z)(\frac{1}{4}+y-z)+2(\frac{1}{4}-x+z)(\frac{1}{4}-y-z))
^{2}-4z^{2} \leq \frac{1}{2})
(đpcm)
Đẳng thức xảy ra
Ví dụ 5.Cho
thỏa mãn
CMR
Lời giải.Do
nên ta đặt
với
Ta có
^{2}+(b-x)^{2}+(a+x)(b-x)=(a-b+\frac{x}{2})^{2}+\frac{3x^{2}}{4}+3ab\geq 3ab)
Đẳng thức xảy ra
Ví dụ 6.Cho
và
.CMR
Lời giải.Vì
nên ta đặt
(
)
^{2}+2(3+t+u)^{2}+8(3+t+u)=62+2(t+u)^{2}+5t^{2}+20u>62)
Ta có đpcm
Ví dụ 7Cho
. Tìm GTNN của
Lời giải.Đặt
thì
Ta có
^{2}+(2+a+b)^{2}+3(1-a)(2+a+b))
^{2}+\frac{3b^{2}}{4}+\frac{9b}{2}+\frac{27}{4} \geq \frac{27}{4})
Đẳng thức xảy ra
Ví dụ 8 Cho
.CMR
Lời giải.Đặt
thì
(
)
^{3}-(1-w)^{3}-6(2+w)^{2}-(1-w)^{2}+9(2+w) \geq0)
^{2} \geq 0)
(đúng)
Đẳng thức xảy ra
{
}
\in)
{
,(0;3))
}
đơn giản vì đây là dạng toán ''mới mẻ'' với các bạn và khi giải các bài toán B.Đ.T các
bạn thường cảm thấy ''lúng túng'' không biết phải sử dụng phương pháp gì?Tuy nhiên,
trong nhiều bài toán B.Đ.t có điều kiện chúng ta có thể dựa vào điều kiện của biến để
đặt ẩn phụ đưa bài toán về dạng đơn giản có thể đánh giá được trực tiếp mà không cần
sử dụng đến các công cụ ''đao to búa lớn''. Bài viết dưới đây dựa trên ý tưởng của
My Teacher-thầy Hoàng văn Đắc
Chúng ta bắt đầu với một bài toán đơn giản sau
Ví dụ 1 .CMR Với
Nhận xét rằng một biểu thức nhiều biến thường đạt giá trị lớn nhất hay nhỏ nhất khi tất
cả các biến bằng nhau ( tổng quát hơn là trường hợp một số biến bằng nhau) hoặc một
số biến có giá trị trên biên .Điều này gợi ý cho ta cách đổi biến như sau
Lời giải Do
Ta có
Đẳng thức xảy ra
đưa bài toán về dạng đơn giản có thể đánh giá trực tiếp được và B.Đ.T chúng ta sử dụng chỉ là
B.Đ.T cơ bản nhất
Chúng ta sẽ gặp lại nhau sau ít phút quảng cáo
Trở lại với bài viết .Tiếp theo chúng ta xem xét một vài ví dụ khác.Qua đó hi vọng
các bạn học sinh THCS sẽ có được một cách nhìn mới với những bài toán B.Đ.T kiểu này.
Ví dụ 2.Cho
Lời giải. Đặt
B.Đ.T cần chứng minh tương đương với
đúng vì
Đẳng thức xảy ra
Ví dụ 3.Cho
CMR
Lời giải.Vì
Ta có
Đẳng thức xảy ra
Ví dụ 4.Cho
Lời giải.Vì
Ta có
Đẳng thức xảy ra
Ví dụ 5.Cho
CMR
Lời giải.Do
Ta có
Đẳng thức xảy ra
Ví dụ 6.Cho
Lời giải.Vì
Ta có đpcm
Ví dụ 7Cho
Lời giải.Đặt
Ta có
Đẳng thức xảy ra
Ví dụ 8 Cho
Lời giải.Đặt
Đẳng thức xảy ra
