Tớ giải lại nhé, xem có đúng không:
- Lấy 4 trong 20 điểm bất kì ⇒ có 20C4 cách.
- Gọi a là trục đối xứng của (O) ⇒ mỗi hình thang cân tạo thành nhận a làm trục đối xứng.
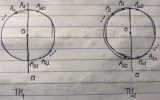
* TH1:
- Kẻ a đi qua 2 đỉnh ⇒ có 10 cách.
- Trên 1 nửa mặt phẳng bờ a, chọn 2 trong 9 đỉnh ⇒ có 9C2 cách.
- Chọn 2 đỉnh khác tương ứng đối xứng với 2 đỉnh đã chọn qua a ⇒ có 1 cách.
⇒ Số hình thang cân là: 10 · 9C2
* TH2:
- Kẻ a chia (O) thành 2 nửa sao cho: 10 điểm trên nửa đường tròn này tương ứng đối xứng với 10 điểm trên nửa đường tròn kia ⇒ có 10 cách.
- Trên 1 nửa mặt phẳng bờ a, chọn 2 trong 10 đỉnh không thuộc a ⇒ có 10C2 cách.
- Chọn 2 đỉnh khác tương ứng đối xứng với 2 đỉnh đã chọn qua a ⇒ có 1 cách.
⇒ Số hình thang cân là: 10 · 10C2
* Trong 2 TH trên, số hình thang cân có 2 trục đối xứng (hay hình chữ nhật) đã được tính 2 lần.
- Số đường kính của (O) đi qua 2 đỉnh là 10.
- Chọn 2 đường kính như trên ⇒ có 10C2 cách. 4 đỉnh thuộc 2 đường kính này chính là 4 đỉnh của 1 hình chữ nhật.
⇒ Số hình chữ nhật là: 10C2
Vậy xác suất là: (10 · 9C2 + 10 · 10C2 - 10C2) / 20C4 = 3/19
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


