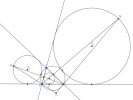
Gọi [imath]J[/imath] là tâm vị tự trong của [imath](I),(O)[/imath].
Ta có bổ đề: [imath]AJ,AD[/imath] đẳng giác trong góc [imath]BAC[/imath].
Chứng minh: Gọi [imath]X[/imath] là điểm tiếp xúc của đường tròn A - mix trong. [imath]T[/imath] là tiếp điểm của đường tròn bàng tiếp góc [imath]A[/imath] với [imath]BC[/imath].
Kẻ đường cao [imath]AH[/imath] của [imath]\Delta ABC[/imath].
Gọi [imath]d[/imath] là đường đẳng giác với [imath]AD[/imath] trong góc [imath]BAC[/imath].
Ta có kết quả quen thuộc [imath](AH,AI,AD,AT) = -1[/imath]. Lấy phép đối xứng trục [imath]AI[/imath] ta có [imath](AO,AI,d, AX) = -1[/imath].
Mặt khác [imath]AX[/imath] đi qua tâm vị tự ngoài của [imath](O),(I)[/imath] nên [imath]d[/imath] đi qua tâm vị tự trong của hai đường tròn này
[imath]\Rightarrow J\in d[/imath]. Bổ đề được chứng minh.
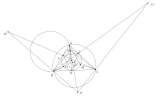
Trở lại bài toán: Xét phép nghịch đảo đối xứng cực [imath]C[/imath], phương tích [imath]CA.CB[/imath] biến [imath]M[/imath] thành [imath]M'[/imath] thuộc [imath](I)[/imath] sao cho [imath]CM',CM[/imath] đẳng giác.
Điểm [imath]N'[/imath] được xác định tương tự. Thế thì theo bổ đề, [imath]J[/imath] là giao của [imath]CM'[/imath] và [imath]BN'[/imath].
Đoạn thẳng [imath]AJ[/imath] cắt [imath](I)[/imath] tại điểm [imath]U[/imath] thì [imath]AU,AD[/imath] đẳng giác.
Vì [imath]J[/imath] là tâm vị tự trong của [imath](O),(I)[/imath] nên dễ dàng chứng minh được [imath]A,U,M',C[/imath] và [imath]A,U,N',B[/imath] đồng viên.
Lấy [imath]P'\in AU[/imath] sao cho [imath]U,B,C, P'[/imath] đồng viên.
Từ kết quả của phép nghịch đảo đối xứng ta có [imath]\Delta CM'A\backsim\Delta CBM\Rightarrow \angle CBM = \angle CM'A = \angle CUA=180^\circ - \angle CBP'[/imath]
[imath]\Rightarrow P'\in BM[/imath]. Tương tự [imath]P'\in CN[/imath].
Hay [imath]P'\equiv P[/imath]. Ta có điều phải chứng minh.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
