- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. mặt cầu
Tập hợp các điểm M trong không gian cách điểm O cố định một khoảng không đổi R được gọi là mặt cầu tâm O, bán kính R.
kí hiệu: [tex]S(O;R)=\left \{ M|OM=R \right \}[/tex] hoặc (S).
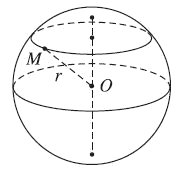
* Đoạn thẳng nối hai điểm nằm trên mặt cầu gọi là dây cung của mặt cầu.
* Dây cung đi qua tâm gọi là đường kính.
ví dụ: cho các điểm A, B, C cố đinh. tập hợp các điểm M thay đổi sao cho [tex]|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|=a[/tex]. biết tập hơp các điểm M tạo thành 1 mặt cầu, tìm bán kính mặt cầu đó.
giải: ta sẽ tìm bán kính mặt cầu theo định nghĩa của mặt cầu.
gọi O là trọng tâm tam giác ABC. do A, B, C cố định nên O cũng cố định.
ta có:
[tex]|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|=|3\overrightarrow{MO}+(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})|=|3\overrightarrow{MO}+\overrightarrow{0}|=3MO=a<=>MO=\frac{a}{3}[/tex]
vậy, M là tập hợp các điểm trong không gian cách O một khoảng là [tex]\frac{a}{3}[/tex]
bán kính của mặt cầu là [tex]\frac{a}{3}[/tex]
2. điểm và mặt cầu
xét điểm A và mặt cầu (S) tâm O, bán kính R.
- nếu OA=R thì A nằm trên mặt cầu.
- nếu OA<R thì A nằm bên trong mặt cầu.
- nếu OA>R thì A nằm bên ngoài mặt cầu.
* nếu A nằm ngoài mặt cầu:
+ qua A có vô số tiếp tuyến với mặt cầu.
+ độ dài nối các đoạn từ A điến tiếm điểm đểu bằng nhau.
+ Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
3. khối cầu
- khối cầu là phần không gian bị giới hạn bởi một mặt cầu, kể cả mặt cầu đó.
- diện tích xung quanh của mặt cầu: [tex]S=4.\pi .R^2[/tex]
- thể tích khối cầu: [tex]V=\frac{4}{3}\pi.R^3[/tex]
4. vị trí tương đối giữa mặt phẳng và mặt cầu
xét mặt phẳng (P) và mặt cầu (S) tâm O, bán kính R.gọi H là hình chiếu vuông góc của O lên mặt phẳng (P).
[tex]h=OH=d(O,(P))[/tex]
- h> R: mặt phẳng (P) và mặt cầu (S) không có điểm chung.
- h=R: mặt phẳng (P) tiếp xúc mặt cầu (S) tại tiếp điểm H. mặt phẩng (P) gọi là tiếp diện của mặt cầu (S).
- h<R: mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính [tex]r=\sqrt{R^2-h^2}[/tex] và cách tâm O một khoảng là h.
+ chu vi đường tròn: [tex]C=2\pi.\sqrt{R^2-h^2}[/tex]
+ diện tích hình tròn: [tex]S=\pi.(R^2-h^2)[/tex]
+ diện tích chỏm cầu: [tex]S=2\pi.R(R-h)[/tex] hoặc [tex]S=\pi.(R^2-h^2+(R-h)^2)[/tex]
Tập hợp các điểm M trong không gian cách điểm O cố định một khoảng không đổi R được gọi là mặt cầu tâm O, bán kính R.
kí hiệu: [tex]S(O;R)=\left \{ M|OM=R \right \}[/tex] hoặc (S).
* Đoạn thẳng nối hai điểm nằm trên mặt cầu gọi là dây cung của mặt cầu.
* Dây cung đi qua tâm gọi là đường kính.
ví dụ: cho các điểm A, B, C cố đinh. tập hợp các điểm M thay đổi sao cho [tex]|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|=a[/tex]. biết tập hơp các điểm M tạo thành 1 mặt cầu, tìm bán kính mặt cầu đó.
giải: ta sẽ tìm bán kính mặt cầu theo định nghĩa của mặt cầu.
gọi O là trọng tâm tam giác ABC. do A, B, C cố định nên O cũng cố định.
ta có:
[tex]|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|=|3\overrightarrow{MO}+(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})|=|3\overrightarrow{MO}+\overrightarrow{0}|=3MO=a<=>MO=\frac{a}{3}[/tex]
vậy, M là tập hợp các điểm trong không gian cách O một khoảng là [tex]\frac{a}{3}[/tex]
bán kính của mặt cầu là [tex]\frac{a}{3}[/tex]
2. điểm và mặt cầu
xét điểm A và mặt cầu (S) tâm O, bán kính R.
- nếu OA=R thì A nằm trên mặt cầu.
- nếu OA<R thì A nằm bên trong mặt cầu.
- nếu OA>R thì A nằm bên ngoài mặt cầu.
* nếu A nằm ngoài mặt cầu:
+ qua A có vô số tiếp tuyến với mặt cầu.
+ độ dài nối các đoạn từ A điến tiếm điểm đểu bằng nhau.
+ Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
3. khối cầu
- khối cầu là phần không gian bị giới hạn bởi một mặt cầu, kể cả mặt cầu đó.
- diện tích xung quanh của mặt cầu: [tex]S=4.\pi .R^2[/tex]
- thể tích khối cầu: [tex]V=\frac{4}{3}\pi.R^3[/tex]
4. vị trí tương đối giữa mặt phẳng và mặt cầu
xét mặt phẳng (P) và mặt cầu (S) tâm O, bán kính R.gọi H là hình chiếu vuông góc của O lên mặt phẳng (P).
[tex]h=OH=d(O,(P))[/tex]
- h> R: mặt phẳng (P) và mặt cầu (S) không có điểm chung.
- h=R: mặt phẳng (P) tiếp xúc mặt cầu (S) tại tiếp điểm H. mặt phẩng (P) gọi là tiếp diện của mặt cầu (S).
- h<R: mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính [tex]r=\sqrt{R^2-h^2}[/tex] và cách tâm O một khoảng là h.
+ chu vi đường tròn: [tex]C=2\pi.\sqrt{R^2-h^2}[/tex]
+ diện tích hình tròn: [tex]S=\pi.(R^2-h^2)[/tex]
+ diện tích chỏm cầu: [tex]S=2\pi.R(R-h)[/tex] hoặc [tex]S=\pi.(R^2-h^2+(R-h)^2)[/tex]
