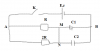
Nguồn điện có suất điện động E và điện trở trong r = R/2 ; các tụ có điện dung C, ban đầu chưa tích điện. Đóng K:
a/ Tính điện tích mỗi tụ
b/ Tính công của nguồn khi tích điện cho tụ
c/ Tính nhiệt lượng tỏa ra cho cả mạch
d/ Tìm cường độ dòng điện chạy qua dây MN trong 0,5 micro giây
e/ Tính nhiệt lượng tỏa ra trên R
View attachment 167783View attachment 167783
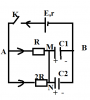
a/ Điện tích mỗi tụ
q1 = C.Umb = C.Uab = C.E
q2 = C.Unb = Uab = CE
b/ Ban đầu tụ chưa tích điện => q1=q2=0
Sau khi K đóng, tổng điện tích trên 2 tụ: q = q1+q2=2CE
=> Điện lượng qua nguồn: [tex]\Delta q=2CE[/tex]
Công của nguồn: [tex]Ang = \Delta q.E=2CE^2[/tex]
c/ Ban đầu các tụ chưa tích điện nên không có năng lượng => W =0
Sau khi đóng K, năng lượng trên 2 tụ: [tex]W'=\frac{1}{2}.CE^2.2=CE^2[/tex]
Nhiệt lượng tỏa ra: [tex]Q=Ang - (W'-W)=CE^2[/tex]
d/ Tổng điện lượng chạy qua R và 2R là 2CE
=> [tex]\Delta qR+\Delta q2R=2CE[/tex]
Mặt khác: q tỉ lệ thuận với R => [tex]\Delta qR=2\Delta q2R[/tex]
=> [tex]\Delta qR=\frac{4}{3}CE ; \Delta q2R=\frac{2}{3}CE[/tex]
Lượng điện tích chạy qua dây MN:
[tex]\Delta qmn=\Delta qR-q1=\frac{4}{3}CE-CE=\frac{1}{3}CE[/tex]
Cường độ dòng điện qua dây MN:
[tex]Imn = \frac{\Delta qmn}{\Delta t}=\frac{CE}{1,5.10^{-6}}(A)[/tex]
e/- Dòng qua r và qua cụm (R//2R) bằng nhau
=> [tex]\left\{\begin{matrix} Qr+Q3R=Q=CE^2 & \\ \frac{Qr}{Q3R}=\frac{\frac{R}{2}}{\frac{2R}{3}}=\frac{3}{4} & \end{matrix}\right. =>\left\{\begin{matrix} Qr=\frac{3CE^2}{7} & \\ Q3R=\frac{4CE^2}{7} & \end{matrix}\right.[/tex]
- Hiệu điện thế 2 đầu R và 2R bằng nhau ( vì R//2R)
=> [tex]\left\{\begin{matrix} QR+Q2R=Q3R=\frac{4CE^2}{7} & \\ \frac{QR}{Q2R}=\frac{2R}{2}=2 & \end{matrix}\right. =>QR=\frac{8CE^2}{21}[/tex]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Hocmai Forum 
