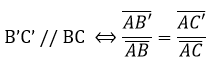[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Lý thuyết Hệ trục tọa độ
1. Trục tọa độ
Một đường thẳng được gọi là trục tọa độ (hay gọi tắc là trục) nếu trên đó đã chọn một điểm O làm gốc và vectơ i→ có độ dài bằng 1 là vectơ đơn vị. Hướng của vectơ i→ là hướng của trục. chẳng hạn, ta có trục x’Ox thì hướng của i→ là x’x.
2. Tọa độ của vectơ trên trục
- Cho vectơ u→ nằm trên trục x’Ox. Vì u→ cùng phương với i→ nên tồn tại duy nhất số thực x sao cho u→=xi→, x được gọi là tọa độ của vectơ u→. Kí hiệu u→=(x) hoặc đơn giản u→(x) để chỉ vectơ u→ có tọa độ x.
+ Rõ ràng, u→ cùng hướng với i→ khi và chỉ khi x ≥ 0 ;
u→ ngược hướng với i→ khi và chỉ khi x ≤ 0 ;
+ Vectơ – không có tọa độ bằng 0.
- Tọa độ của vectơ AB→ được gọi là độ dài đại số của vectơ AB→, kí hiệu là:
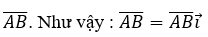
3. Tọa độ của điểm trên trục
- Cho điểm M trên trục x’Ox. Tọa độ của vectơ OM→ cũng được gọi là tọa độ của điểm M, kí hiệu M(x). Đôi khi để cho thuân tiện người ta còn dùng kí hiệu:
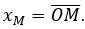
- Độ dài đại số của một vectơ trên trục được tính theo tọa độ của điểm đầu và tọa độ điểm cuối:
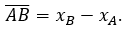
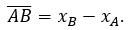
4. Hệ trục tọa độ Đề - các
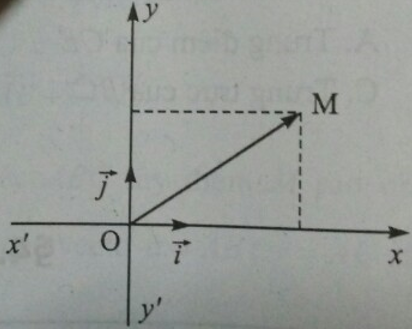
- Cho hai trục x’Ox, y’Oy vuông góc với nhau tại gốc chung O. Hệ hai trục xác định như trên gọi hệ trục tọađộ Oxy (hệ trục tọa độ Đề - các vuông góc); x’Ox là trụ hoành, y’Oy là là trục tung, O là gốc của hệ trục (gốc tọa độ).
- Mặt phẳng có gắn hệ trục tọa độ như trên gọi là mặt phẳng tọa độ.
5. Tọa độ của vectơ
- Cho mặt phẳng tọa độ Oxy với các vectơ đơn vị của trục hoành và trục tung lần lượt là i→, j→ . Vì i→và j→ không cùng phương nên với mỗi vectơ u→ trên mặt phẳng tọa độ, tồn tại suy nhất cặp số (x ; y) sao cho u→ = xi→ + yj→.
Cặp số (x; y) được gọi là tọa độ của vectơ u→ (x là hoành độ, y là tung độ) , kí hiệu u→=(x;y) hoặc u→(x;y).
- Cho hiệu u→ = (x;y) , u'→=(x';y' ). Ta có:
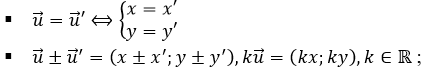
Tổng quát, αu→ + βu'→=(αx+βx', αy+βy' ) ∀α,β ∈ R .
6. Tọa độ của điểm
- Cho điểm M trên mặt phẳng tọa độ Oxy. Tọa độ của vectơ OM→ được gọi là tọa độ của điểm M.
Để biểu thị M có tọa độ (x ; y) ta viết M = (x ; y) hoặc đơn giản M(x; y). Ta cũng dùng kí hiệu xN ,yMđể chỉ hoành độ và tung độ của điểm M.
M = (x; y) <=> OM→=(x;y).
- Tọa độ của vectơ tính theo tọa độ điểm đầu và điểm cuối:
AB→=(xB-xA; yB-yA )
- Trung điểm I của đoạn thẳng MN có tọa độ :
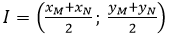
- Trọng tâm G của tam giác ABC có tọa độ:
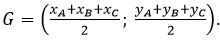
7. Kiến thức mở rộng
Định lí Ta – lét (dưới dạng độ dài đại số) : Cho tam giác ABC. Các điểm B’, C’ theo thứ tự thuộc các đường thẳng AB, AC. Ta có:
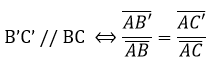
1. Trục tọa độ
Một đường thẳng được gọi là trục tọa độ (hay gọi tắc là trục) nếu trên đó đã chọn một điểm O làm gốc và vectơ i→ có độ dài bằng 1 là vectơ đơn vị. Hướng của vectơ i→ là hướng của trục. chẳng hạn, ta có trục x’Ox thì hướng của i→ là x’x.
2. Tọa độ của vectơ trên trục
- Cho vectơ u→ nằm trên trục x’Ox. Vì u→ cùng phương với i→ nên tồn tại duy nhất số thực x sao cho u→=xi→, x được gọi là tọa độ của vectơ u→. Kí hiệu u→=(x) hoặc đơn giản u→(x) để chỉ vectơ u→ có tọa độ x.
+ Rõ ràng, u→ cùng hướng với i→ khi và chỉ khi x ≥ 0 ;
u→ ngược hướng với i→ khi và chỉ khi x ≤ 0 ;
+ Vectơ – không có tọa độ bằng 0.
- Tọa độ của vectơ AB→ được gọi là độ dài đại số của vectơ AB→, kí hiệu là:
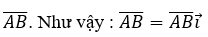
3. Tọa độ của điểm trên trục
- Cho điểm M trên trục x’Ox. Tọa độ của vectơ OM→ cũng được gọi là tọa độ của điểm M, kí hiệu M(x). Đôi khi để cho thuân tiện người ta còn dùng kí hiệu:
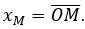
- Độ dài đại số của một vectơ trên trục được tính theo tọa độ của điểm đầu và tọa độ điểm cuối:
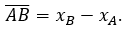
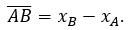
4. Hệ trục tọa độ Đề - các
- Cho hai trục x’Ox, y’Oy vuông góc với nhau tại gốc chung O. Hệ hai trục xác định như trên gọi hệ trục tọađộ Oxy (hệ trục tọa độ Đề - các vuông góc); x’Ox là trụ hoành, y’Oy là là trục tung, O là gốc của hệ trục (gốc tọa độ).
- Mặt phẳng có gắn hệ trục tọa độ như trên gọi là mặt phẳng tọa độ.

5. Tọa độ của vectơ
- Cho mặt phẳng tọa độ Oxy với các vectơ đơn vị của trục hoành và trục tung lần lượt là i→, j→ . Vì i→và j→ không cùng phương nên với mỗi vectơ u→ trên mặt phẳng tọa độ, tồn tại suy nhất cặp số (x ; y) sao cho u→ = xi→ + yj→.
Cặp số (x; y) được gọi là tọa độ của vectơ u→ (x là hoành độ, y là tung độ) , kí hiệu u→=(x;y) hoặc u→(x;y).
- Cho hiệu u→ = (x;y) , u'→=(x';y' ). Ta có:
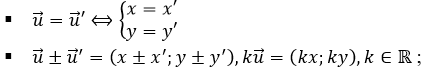
Tổng quát, αu→ + βu'→=(αx+βx', αy+βy' ) ∀α,β ∈ R .
6. Tọa độ của điểm
- Cho điểm M trên mặt phẳng tọa độ Oxy. Tọa độ của vectơ OM→ được gọi là tọa độ của điểm M.
Để biểu thị M có tọa độ (x ; y) ta viết M = (x ; y) hoặc đơn giản M(x; y). Ta cũng dùng kí hiệu xN ,yMđể chỉ hoành độ và tung độ của điểm M.
M = (x; y) <=> OM→=(x;y).
- Tọa độ của vectơ tính theo tọa độ điểm đầu và điểm cuối:
AB→=(xB-xA; yB-yA )
- Trung điểm I của đoạn thẳng MN có tọa độ :
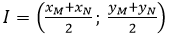
- Trọng tâm G của tam giác ABC có tọa độ:
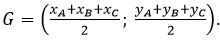
7. Kiến thức mở rộng
Định lí Ta – lét (dưới dạng độ dài đại số) : Cho tam giác ABC. Các điểm B’, C’ theo thứ tự thuộc các đường thẳng AB, AC. Ta có: