Bài này không biết em đã có khái niệm gì về bảo toàn động lượng theo phương chưa nhỉ?
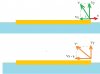
Người nhảy xiên so với đất 1 góc a.
Trên hệ quy chiếu gắn với đất (HQC1), phân tích các vecto vận tốc như hình. u là vận tốc giật lùi của xe trượt.
Trên hệ quy chiếu gắn với xe trượt (HQC2), phân tích được các vecto vận tốc như hình dưới. V' là vận tốc của người so với xe trượt, để vận tốc nhảy là bé nhất thì V' phải có phương hợp với phương ngang một góc 45 độ.
Áp dụng bảo toàn động lượng theo phương ngang, cho HQC 1, ta có. [TEX]mV_x + M.u = 0[/TEX] hay [TEX]mVcosa + M.u = 0[/TEX]
Tính được [TEX]u = - \frac{m.V.cosa}{M}[/TEX]
Xét điều kiện người đáp xuống được mép xe trượt trên HQC2. Thời gian người chuyển động trên không là:
[TEX]t = \frac{V_y}{g} = \frac{2.V.sina}{g}[/TEX]
Trong thời gian đó, theo phương ngang người phải đi được một quãng L so với ván.
[TEX]L = (V_x - u).t = (V.cosa + \frac{m.V.cosa}{M}).\frac{2.V.sina}{g}[/TEX] (1)
Theo điều kiện để vận tốc là nhỏ nhất, V' phải có phương 45 độ nên.
[TEX]V.cosa - u = V_y[/TEX] Hay [TEX]V.cosa + \frac{m.V.cosa}{M} = V.sina[/TEX] (2)
Từ pt (2) tìm được góc a, thay vào pt (1) tìm được vận tốc V. Cái này thay số thôi chứ giải tổng quát tính toán khó lắm.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
