Câu 37.
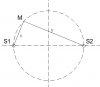
Gọi M là 1 điểm bất kì trên đường tròn. Khoảng cách từ M đến S1 là x, đến S2 là y.
Khi đó ta phải có [TEX]|y - x| = k.\lambda[/TEX]
Lại có M.S1.S2 là tam giác vuông tại M nên. [TEX]x^2 + y^2 = S_1S_2^2 = (5,4\lambda)^2[/TEX]
Giải cho trường hợp y > x (trường hợp x > y sẽ đối xứng với y > x.
Thay [TEX]y = k\lamda + x[/TEX] vào pt dưới được:
[TEX](k\lamda+x)^2 + x^2 = 29,16.\lambda^2[/TEX]
Biến đổi được pt theo x.
[TEX]2x^2 + 2.k.\lambda.x + (k^2\lambda^2 - 29,16\lambda^2) = 0[/TEX]
Lập [TEX]\Delta = (5,4\lambda)^2 - k^2\lambda^2\geq 0[/TEX]
Ta sẽ được [TEX]K \leq 5,4[/TEX]
Vậy k = 0, 1, 2, 3, 4, 5.
Với y > x sẽ đối xứng với nghiệm của x (đối xứng trái - phải). Nên sẽ có 11 điểm trên nửa trên của đường tròn.
Tính cả nửa dưới là 22 điểm tất cả.
Bài 34.
Bài này chắc là giải mò thôi.
Các họa âm sẽ là bội số của âm cơ bản. [TEX]f_h = k.f_{cb}[/TEX]
Vậy tần số âm cơ bản sẽ là ước chung của hai họa âm có tần số 2640 Hz và 4400 Hz.
Với âm cơ bản từ 300 đến 800, ứng với [TEX]f_h= 2640[/TEX] ta tính được k có các giá trị 4, 5, 6, 7, 8.
Lần lượt tính các giá trị của [TEX]f_{cb}[/TEX] ứng với mỗi giá trị k. Giá trị nào là ước số của 4400 thì lấy.
Ta lấy được [TEX]k = 6[/TEX] và [TEX]f_{cb} = 440 Hz[/TEX]
Từ đó, tần số [TEX]20000 Hz[/TEX] ứng với họa âm thứ 45. Vậy có 45 họa âm.
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.