- 5 Tháng sáu 2017
- 157
- 167
- 69
- 23
- Nam Định
- thcs yên hưng
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
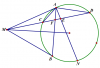
cho đường tròn (O,R) . từ M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA,MB ( A ,B là tiếp điểm ) ,OM =2R .1 cát tuyến bất kì qua M cắt đường tròn tại C và D ( C nằm giữa M,D) . Kẻ tia phân giác của [tex]\widehat{CAD}[/tex] cắt CD tại E và cắt đường tròn tại N . Gọi F là giao điểm của AB và CD
a) OAMB nội tiếp
b) MA=ME
c) [tex]\frac{2}{CD}=\frac{1}{MD}+\frac{1}{FD}[/tex]
a) OAMB nội tiếp
b) MA=ME
c) [tex]\frac{2}{CD}=\frac{1}{MD}+\frac{1}{FD}[/tex]
Last edited: