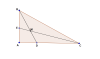
Đặt BC = a ; AC = b ; AB = c
Từ gt: BC.CE= 2 BM.CM
[tex]\Rightarrow \frac{BM}{BD}.\frac{CM}{CE}=\frac{1}{2}[/tex]
(1)
Theo tính chất đường phân giác ta có:
[tex]\frac{CD}{AD}=\frac{BC}{AB}\Rightarrow \frac{CD}{CD+AD}=\frac{BC}{AB+BC}\Rightarrow \frac{CD}{AC}=\frac{BC}{AB+BC}\Rightarrow CD=\frac{AC.BC}{AB+BC }=\frac{ab}{c+a}[/tex]
Theo tính chất đường phân giác ta có:
[tex]\frac{BM}{MD}=\frac{BC}{DC}\Rightarrow \frac{BM}{BM+MD}=\frac{BC}{BC+CD}\Rightarrow \frac{BM}{BD}=\frac{a}{a+\frac{ab}{a+c}}=\frac{a}{\frac{a(a+b+c)} {a+c}}=\frac{b+c}{a+b+c}[/tex]
(2)
Tương tự ta có:
[tex]\frac{CM}{CE} = \frac{b+c}{a+b+c}[/tex]
(3)
Từ (1), (2) , (3) ta có:
[tex]\frac{(a+c)(b+c)}{(a+b+c)^2}=\frac{1}{2} \Leftrightarrow a^2+b^2+c^2+2(ab+bc+ca)= 2(ab+ac+bc+c^2) \Leftrightarrow a^2+b^2=c^2[/tex]
Suy ra tam giác ABC là tam giác vuông ( Định lí Py-ta-go đảo )
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
