cho a,b,c thỏa mãn a+b+c=2018. CMR: a^4+b^4/a^3+b^3 + b^4+c^4/b^3+c^3 + c^4+a^4/c^3+a^3
2018
Phải có thêm điều kiện a,b,c>0 chứ nhỉ -.-
Viết lại đề bài:
Cho a,b,c>0 thỏa mãn a+b+c=2018. Chứng minh rằng: [tex]\frac{a^{4}+b^{4}}{a^{3}+b^{3}}+\frac{b^{4}+c^{4}}{b^{3}+c^{3}}+\frac{c^{4}+a^{4}}{c^{3}+a^{3}}\geq 2018[/tex]
_______________________________
+) Xét bài toán phụ: Với 2 số thực dương x,y ta luôn có: [tex]\frac{x^{4}+y^{4}}{x^{3}+y^{3}}\geq \frac{1}{2}(x+y)[/tex] (*)
Thật vậy: (*) [tex]\Leftrightarrow (x-y)^{2}(x^{2}+xy+y^{2})\geq 0[/tex] luôn đúng
Dấu "=" xảy ra tại x=y
+) Trở lại bài toán chính, áp dụng bài toán phụ ta có:
$\frac{a^{4}+b^{4}}{a^{3}+b^{3}}+\frac{b^{4}+c^{4}}{b^{3}+c^{3}}+\frac{c^{4}+a^{4}}{c^{3}+a^{3}}$[tex]\geq \frac{1}{2}(a+b)+ \frac{1}{2}(b+c)+ \frac{1}{2}(c+a)=a+b+c=2018[/tex] (đpcm)
Đẳng thức xảy ra tại a=b=c=[tex]\frac{2018}{3}[/tex]
#bone: m dịch được đề ah? Bái phục :v
#An: :3 Quá khen quá khen :v Chẳng qua làm rồi thôi, chứ đề viết như này biết hiểu theo cách nào cho đúng =-=
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
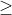2018
