Mi đưa t 50 HMCoin t giải!
4. a) Gọi điểm cố định mà (d) luôn đi qua là A[tex](x_{0};y_{0})[/tex].
[tex]\Rightarrow y_{0}=kx_{0}+3[/tex] (đúng với mọi m)
[tex]\Leftrightarrow x_{0}.k+(3-y_{0})=0[/tex] (đúng với mọi m)
[tex]\Leftrightarrow \left\{\begin{matrix} x_{0}=0\\ 3-y_{0}=0\\ \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x_{0}=0\\ y_{0}=3\\ \end{matrix}\right.[/tex]
Ta được A(0;3) là điểm cố định mà (d) luôn đi qua.
b)
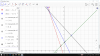
Cho [tex]x=0\rightarrow y=3.[/tex] Ta được B(0;3)
[tex]y=0\rightarrow x=-\frac{3}{k}.[/tex] Ta được [tex]C(-\frac{3}{k};0)[/tex]
Ta có: [tex]\frac{1}{OH^{2}}=\frac{1}{OB^{2}}+\frac{1}{OC^{2}}[/tex]
[tex]\frac{1}{4}=\frac{1}{9}+\frac{1}{(\frac{3}{k})^{2}}[/tex]
[tex]\Rightarrow \frac{k^{2}}{9}=\frac{5}{36}\Rightarrow k=\pm \frac{\sqrt{5}}{2}[/tex]
c) [tex]\frac{1}{OH^{2}}=\frac{1}{OB^{2}}+\frac{1}{OC^{2}}\Rightarrow \frac{1}{OH^{2}}=\frac{1}{9}+\frac{k^{2}}{9}=\frac{k^{2}+1}{9}[/tex]
[tex]\Rightarrow OH^{2}=\frac{9}{k^{2}+1}\leq \frac{9}{1}=9[/tex]
[tex]\Rightarrow OH\leq 3\Rightarrow MaxOH=3[/tex] đạt được tại k=0
6. a)
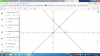
Cho [tex]x=0\rightarrow y=-3.[/tex] Ta được A(0;-3)
[tex]y=0\rightarrow x=\frac{3}{2m+5}.[/tex] Ta được [tex]B(\frac{3}{2m+5};0)[/tex]
Ta có: [tex]\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}[/tex]
[tex]\Rightarrow[/tex] (sai đề)
b) Ta có: [tex]S_{AOB}=2\Rightarrow \frac{OA.OB}{2}=2\Rightarrow 3.\left | \frac{3}{2m+5} \right |=4\Rightarrow \left | \frac{3}{2m+5} \right |=\frac{4}{3}[/tex]
TH1: [tex]2m+5>0\Rightarrow m>-\frac{5}{2}\Rightarrow \frac{3}{2m+5}=\frac{4}{3}\Rightarrow m=-\frac{11}{8}[/tex]
TH2: [tex]2m+5<0\Rightarrow m<-\frac{5}{2}\Rightarrow \frac{3}{2m+5}=-\frac{4}{3}\Rightarrow m=-\frac{29}{8}[/tex]
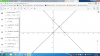
8. a) (+) y=3x+4
Cho [tex]x=0\rightarrow y=4.[/tex] Ta được A(0;4)
(+) [tex]y=-\frac{1}{3}x+2[/tex]
Cho [tex]x=0\rightarrow y=2.[/tex] Ta được C(0;2)
(+) Hoành độ của M là nghiệm của phương trình: [tex]3x+4=-\frac{1}{3}x+2\Rightarrow x=-\frac{3}{5}\rightarrow y=\frac{11}{5}.[/tex] Ta được [tex]M(-\frac{3}{5};\frac{11}{5})[/tex]
[tex]\Rightarrow AC=, CM=, AM=,[/tex] (cái này vẽ hình ra rồi dựa vào hình và nhìn tọa độ của các điểm A, C, M để tính độ dài của các đoạn thẳng đó)
Ta có: [tex]AM^{2}+CM^{2}=AC^{2}\Rightarrow \triangle ACM[/tex] vuông tại M.
b) (+) y=3x+4
Cho [tex]y=0\rightarrow x=-\frac{4}{3}.[/tex] Ta được [tex]B(-\frac{4}{3};0)[/tex]
(+) [tex]y=-\frac{1}{3}x+2[/tex]
Cho [tex]y=0\rightarrow x=6.[/tex] Ta được D(6;0)
OM=(...), OA=4, [tex]\Rightarrow S_{AOM}=\frac{6}{5}[/tex]
[tex]OB=\frac{4}{3}, AB=(...)[/tex] [tex]\Rightarrow S_{AOB}=\frac{8}{3}[/tex]
Với các điểm có tọa độ như trên thì B, O, D thẳng hàng[tex]\Rightarrow[/tex] (sai đề)
22. a) Hàm đồng biến[tex]\Leftrightarrow m-1>0\Leftrightarrow m>1[/tex]
Hàm nghịch biến[tex]\Leftrightarrow m-1<0\Leftrightarrow m<1[/tex]
b) [tex]\left.\begin{matrix} (d)//Ox\\ Ox\perp Oy\\ \end{matrix}\right\} \Rightarrow (d)\perp Oy\Leftrightarrow m-1=0\Leftrightarrow m=1[/tex] (Chỗ này có chút thừa nhận)
c) Thay A(-1;1) ta được: -1=(m-1)+m[tex]\Leftrightarrow m=0[/tex]
d) [tex]x-2y=1\Rightarrow y=\frac{x-1}{2}=\frac{1}{2}x-\frac{1}{2}[/tex] (Đây là cách để đưa về hàm số có dạng y=ax+b)
[tex]\Rightarrow (d)//(d')\Leftrightarrow \left\{\begin{matrix} m-1=\frac{1}{2}\\ m\neq -\frac{1}{2}\\ \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} m=\frac{3}{2}\\ m\neq -\frac{1}{2}\\ \end{matrix}\right. \Leftrightarrow m=\frac{3}{2}[/tex]
e) Thay [tex]A(2-\frac{\sqrt{3}}{2};0)[/tex] ta được:
[tex]0=(m-1)(2-\frac{\sqrt{3}}{2})+m\Leftrightarrow (m-1).\frac{4-\sqrt{3}}{2}+m=0\Rightarrow (m-1)(4-\sqrt{3})+2m=0\Leftrightarrow (6-\sqrt{3})m+(\sqrt{3}-4)=0\Rightarrow m=\frac{6-\sqrt{3}}{4-\sqrt{3}}[/tex]
f) Xem bài 4a)
23. a) Thay A(1;-2) ta được: [tex]-2=(m-2).1+n\Leftrightarrow m+n=1 (1)[/tex]
Thay B(3;-4) ta được: [tex]-4=(m-2).3+n\Leftrightarrow 3m+n=2 (2)[/tex]
Từ (1) và (2)[tex]\Rightarrow m=n=\frac{1}{2}[/tex]
b) Thay [tex]M(0;1-\sqrt{2})[/tex] ta được: [tex]n=1-\sqrt{2}[/tex]
Thay [tex]N(2+\sqrt{2};0)[/tex] ta được: [tex]0=(m-1)(2+\sqrt{2})+n\Rightarrow m-1=\frac{\sqrt{2}-1}{2+\sqrt{2}}\Rightarrow m=\frac{2\sqrt{2}+1}{\sqrt{2}+2}[/tex]
c) (+) [tex]x-2y=3\Rightarrow y=\frac{x-3}{2}=\frac{1}{2}x-\frac{3}{2}(d'')\Rightarrow (d')\perp (d'')\Leftrightarrow (m-2).\frac{1}{2}=-1\Rightarrow m=0[/tex]
(+) [tex]3x+2y=1\Rightarrow y=-\frac{3}{2}x+\frac{1}{2}(d''')\Rightarrow (d')//(d''')\Leftrightarrow \left\{\begin{matrix} m-2=-\frac{3}{2}\\ n\neq \frac{1}{2}\\ \end{matrix}\right.\Rightarrow m=\frac{1}{2}[/tex]
(+) [tex]y-2x+3=0\Leftrightarrow y=2x-3(d)\Rightarrow (d)'\equiv (d)\Leftrightarrow \left\{\begin{matrix} m-2=2\\ n=-3\\ \end{matrix}\right.\Rightarrow m=4[/tex]
Camera trên máy tính chụp vừa mờ lại vừa bị ngược nên đành gõ từ đầu đến cuối!!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
